Ballistic Coefficient calculation
Commonly used nowadays is the ballistic coefficient (BC or G) according to Karpov (i.e. Dr. Boris Karpov, US Army Research Laboratory, 1944), which represents not only the characteristics of the shape and the weight of the bullet, but also takes into account the actual air resistance at a specific velocity.
View attachment 379565
To calculate the ballistic coefficient requires two velocities. The initial velocity (
V0), and then, at a certain point on the trajectory at the distance x from the muzzle, the
Vx velocity. To measure
V0 directly is difficult; therefore
V5 and
V100 were measured, from which
V0 was subsequently extrapolated. The ballistic coefficient for one hundred metres is calculated using the following formula, in which x = 100 m. Similarly this is also applicable, of course, to other distances.
The ballistic coefficient was not adjusted in accordance with the altitude and should be considered as being universal, since Sellier & Bellot's ballistic testing laboratory is 400 m asl., which corresponds to the average altitude of the Czech Republic. A distance of one hundred metres was chosen because, at this distance, S&B also checks the accuracy of the ammunition and because this distance has long been considered as being a "hunting" distance. The actual tests were carried out in such a manner that, using the same series of ammunition, first
V5 and subsequently
V100 were shot from the same barrel. Since the shooting was not performed simultaneously, firing was repeated with other series and the uniformity of the results was monitored. The ammunition was always tempered to +21 ºC.
BCs are calculated to three decimal places, which is in practice is completely satisfactory. Even after correcting for the atmospheric conditions and the altitude, the weight tolerance of the bullet and its initial velocity (
V0) still come into play, and of course so does the length and the wear of the specific barrel.
The entire issue is actually much broader, because, for example, on the Internet it is possible to find articles that describe differences of up to 25% from the values reported by the manufacturer and discovered in the case of overshoot.
The values specified by S&B correspond very well with reality, because the velocity at a distance of 100 metres was measured and also because it is not a result that is based on a single firing. Also the documentation provided by the Sierra Company can be accepted as being reliable. The results, however, for the reasons described in the preceding paragraph, cannot be taken as dogma.
https://www.sellier-bellot.cz/en/products/ballistic-coefficient-calculation/
________________________________________________________________________________________________________________________________________________________
Differing mathematical models and bullet ballistic coefficients
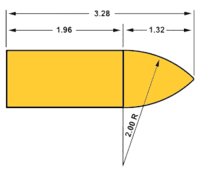
G1 shape standard projectile. All measurements in calibers/diameters.
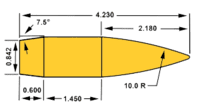
G7 shape standard projectile. All measurements in calibers/diameters.
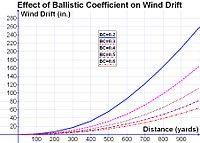
Wind drift calculations for rifle bullets of differing G1 BCs fired with a muzzle velocity of 2,950 ft/s (900 m/s) in a 10 mph (4.5 m/s; 16 km/h) crosswind.
[58]
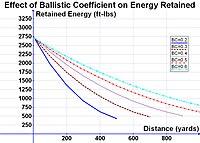
Energy calculations for 9.1 grams (140 gr) rifle bullets of differing G1 BCs fired with a muzzle velocity of 2,950 feet per second (900 m/s).
[59]
Most ballistic mathematical models and hence tables or software take for granted that one specific drag function correctly describes the drag and hence the flight characteristics of a bullet related to its ballistic coefficient. Those models do not differentiate between
wadcutter, flat-based,
spitzer, boat-tail,
very-low-drag, etc. bullet types or shapes. They assume one invariable drag function as indicated by the published BC. Several different drag curve models optimized for several standard projectile shapes are available, however.
The resulting drag curve models for several standard projectile shapes or types are referred to as:
- G1 or Ingalls (flatbase with 2 caliber (blunt) nose ogive - by far the most popular)[60]
- G2 (Aberdeen J projectile)
- G5 (short 7.5° boat-tail, 6.19 calibers long tangent ogive)
- G6 (flatbase, 6 calibers long secant ogive)
- G7 (long 7.5° boat-tail, 10 calibers secant ogive, preferred by some manufacturers for very-low-drag bullets[61])
- G8 (flatbase, 10 calibers long secant ogive)
- GL (blunt lead nose)
Since these standard projectile shapes differ significantly the G
x BC will also differ significantly from the G
y BC for an identical bullet.
[62] To illustrate this the bullet manufacturer Berger has published the G1 and G7 BCs for most of their target, tactical, varmint and hunting bullets.
[63] Other bullet manufacturers like Lapua and Nosler also published the G1 and G7 BCs for most of their target bullets.
[64][65] How much a projectile deviates from the applied reference projectile is mathematically expressed by the form factor (
i). The applied reference projectile shape always has a form factor (
i) of exactly 1. When a particular projectile has a sub 1 form factor (
i) this indicates that the particular projectile exhibits lower drag than the applied reference projectile shape. A form factor (
i) greater than 1 indicates the particular projectile exhibits more drag than the applied reference projectile shape.
[66] In general the G1 model yields comparatively high BC values and is often used by the sporting ammunition industry.
[65]
Courtesy of Wikipedia
_________________________________________________________________________________________________________________________________________________________________________________________________________
Ballistic Calculator:
https://www.jbmballistics.com/cgi-bin/jbmbcv-5.1.cgi






