Applied Ballistics For Long Range Shooting
By Bryan Litz
The previous chapter presented a model for the lethality of hunting bullets which is one of the limiting factors in long range hunting. This chapter focuses on the other major constraint which is accuracy. Once you’ve determined the approximate maximum lethal range of your selected rifle and bullet, it’s important to understand the uncertainties involved which may cause you to miss your aimpoint. Accuracy is obviously a very important factor in long range hunting. Not only do you have to hit the animal, but you have to hit it in a vital area which is a small percentage of the animal’s total size. If you are accurate enough and can reliably place shots within the small vital area of your target, you can effectively increase the lethal range with superior shot placement
Accounting for uncertainty
Long range shooting has many variables. Most of the variables can be measured and accounted for. These are known as deterministic variables. Examples of deterministic variables are: gravity drop, range, atmospherics, rifle cant (tilt), and spin drift. Every deterministic variable can be quantified and corrected for. If all variables were deterministic, shooters would only be limited by their rifles inherent precision (grouping ability). For example, if a rifle was capable of 10” groups at 1000 yards, you could expect to be able to reliably hit a 10” target at 1000 yards, etc. Long range shooters know that in reality, you cannot count on perfect shot placement. The reason why you can’t is because of the non-deterministic variables involved in long range shooting. Non-deterministic variables are those variables that cannot be measured precisely or calculated for each shot.
The two biggest non-deterministic variables remaining in long range shooting are wind determination and muzzle velocity variation. Furthermore, there are the effects introduced by firing from a cold bore.
The following analysis will proceed with the assumption that the shooter has measured and accounted for all of the deterministic variables, and will focus on the effects of the non-deterministic variables.
Figure 15.1 illustrates how the non-deterministic effects of muzzle velocity variation and wind deflection combine to shape a likely impact zone for a given set of non-deterministic variables. The goal is to determine the size and shape of the impact zone under the influence of some non-deterministic variables.
Step 1: Establish the baseline.
This is the inherent precision ability of the rifle and can be determined by averaging groups at short range. It’s important to be honest with this part. The goal is to represent the average grouping potential of the rifle, not the best ever 3 shot group. A good way to establish the baseline is to average 5 groups of 5 shots each. This will give a good representation of the rifles inherent precision. Contrary to the belief of many gun writers and shooters, a single 3-shot group is worthless for determining the grouping potential of any rifle.
For this example, we’ll consider a 30-06 rifle shooting 185 grain bullets at an average muzzle velocity of 2850 fps. The rifle will be modeled as being capable of 1” groups at 100 yards on average. For this current analysis, we’ll consider the impact zone at 500 yards. According to the principles of bullet dispersion given in Chapter 11, we can extrapolate the group size from 100 yards to 500 yards based on the bullets time of flight. The bullets time of flight at 100 yards is 0.1084 seconds, and at 500 yards, it’s 0.6154 seconds. Since the rifle is capable of grouping into 1 inch at 100 yards, we can expect the dispersion to produce a 500 yard group of: 1 inch times 0.6154/0.1084 = 5.7 inches minimum.
The next piece of information we need is the extreme spread of muzzle velocity variation for the load under consideration. The extreme spread (ES) should be mesured for as many shots as possible; at least 10 shots should make up the sample. Alternatively, you can use 4 times the standard deviation as a representation of the muzzle velocity extreme spread (+/- 2 standard deviations represents 95% confidence limits). This statistical data gathered on the muzzle velocity will be used to characterize the uncertainty of this non-deterministic variable so that we can correlate it to an expected vertical dispersion. For this example, we’ll use an extreme spread of 60 fps in muzzle velocity. That would roughly correlate to a standard deviation of about 15 fps.
So the raw parameters we’ll be using to create the impact zone analysis at 500 yards are:
• Rifle capable of averaging 1” groups at 100 yards: extrapolates to 5.7 inches minimum at 500 yards.
• 60 fps extreme spread in muzzle velocity
• +/- 2 mph uncertainty in crosswind speed
The rifle’s inherent precision and the extreme spread of muzzle velocity can be considered relatively constant values whereas the uncertainty in wind speed is something that could be different for each shot.
Step 2: Turn the raw uncertainties into inches of deflection at the target range.
This can easily be done with the included software. We’ll do the vertical plane first. Using all of the pertinent variables, calculate the drop at 500 yards for the average muzzle velocity. The 185 grain bullets at 2850 fps will have about 49” of drop at 500 yards from a 100 yard zero. Now add ½ of the extreme spread to the muzzle velocity to see what the difference in drop is. An additional 30 fps in muzzle velocity would cause a round to hit about 1.2” higher at 500 yards, so you can expect +/- 1.2”, or 2.4” of vertical spread in addition to the 5.7” inherent precision of the rifle at 500 yards.
Now here comes a little twist. In order to quantify the total vertical dispersion, you can’t simply add the 5.7” and 2.4”. The likely magnitude of multiple random errors is quantified using the RSS method which stands for Root Sum Squares. Mathematically, the sum is written as:
Where a and b are the two components being added. In this case, the total likely vertical dispersion is:
So the likely total vertical dispersion from the rifles inherent precision and the velocity variation is 6.2” total.
Now let’s consider the horizontal plane.
We have estimated +/- 2 mph of crosswind uncertainty for this example. Again, using the ballistics program, convert this wind uncertainty to inches of deflection for the pertinent variables. In this case, a 2 mph crosswind will result in +/- 3.1” of wind deflection at 500 yards, a total horizontal error of 6.2”. The RSS of the horizontal components of dispersion yields:
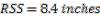
So the likely total horizontal dispersion is +/- 4.2 inches, or 8.4 inches total at 500 yards with the non-deterministic variables we’re using in this example. This information is best represented visually. Refer to Figure 15.1 for an illustration of the expected cumulative dispersion.
Notice how the muzzle velocity variation adds some uncertainty to the vertical shape of the group, and the wind uncertainty adds some uncertainty to the horizontal shape. The probability contour in the bottom right corner of Figure 15.1 shows the regions and associated probability of impacts. For example, there is a 67% chance the rounds will strike the inner ring (2.1 inches tall by 2.8 inches wide), a 95% chance that the rounds will strike in the next biggest ring (4.1 inches tall and 5.6 inches wide), and a 99% chance the rounds will strike in the largest ring (6.2 inches tall by 8.4 inches wide).
Publisher's Note: The book can be purchased at the LRH Gear Shop
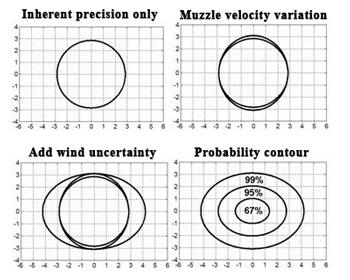
Figure 15.1. Cumulative effects of non-deterministic variables on a 500 yard target.
It’s very important to remember that this analysis assumes that all of the deterministic variables are accounted for. If the rifle is slightly canted, spin drift unaccounted for, shot taken from a poorly supported position, sights not properly calibrated and adjusted, zero not accurately set, etc etc, the impact zone will be the same size, but it will not be centered on the aim point which will likely result in a miss. Figure 15.2 shows the likely impact zone from the previous example and its relative size on the vital area of a deer; as well as the effects of having an unaccounted for deterministic variable.
To view a 3 minute video synopsis of the book by the author CLICK HERE AND THEN PAGE DOWN
As illustrated in Figure 15.2, if all the deterministic variables are accounted for, then the uncertainty introduced by the muzzle velocity variation and wind uncertainty isn’t enough to cause a miss on a typical white tailed deer at 500 yards (left). However, if the deterministic variables are not perfectly accounted for, the impact zone can be offset from the aim point and result in a miss. The example in Figure 15.2 has the impact zone shifted by about 15 inches. At 500 yards, if the rifle is canted by just 5 degrees, it will cause the point of impact to shift laterally by 4.3 inches in this example. In contrast, spin drift is only worth about 1.4 inches at this range. The most likely cause of offsetting the aim point in a hunting situation is the combination of not having a perfectly steady platform to shoot from, and being excited about the shot. These real world effects can easily compromise shot placement as much as any other variable.
Figure 15.2. If all of the deterministic variables are accounted for, the impact zone will be centered on the aim point. However if the deterministic variables are unaccounted for the impact zone will be offset and a miss can result.
In the above analysis, the ballistic performance of the rifle/bullet comes into play in the step where you translate the non-deterministic variables into physical displacement on the target. The better the ballistic performance of your bullets, the less wind deflection you will incur from a given uncertainty of crosswind speed. Seeing as how wind is usually the greatest non-deterministic variable, ballistic performance turns out to play quite an important role in the size of the expected impact zone. Furthermore, improved inherent precision of the rifle and more consistent muzzle velocities will serve to further shrink the size of the expected impact zone. However, taking another look at Figure 15.2 for the 500 yard shot on a deer, it’s clear that the impact zone is small enough to insure a pretty reliable hit on a deer sized target. Therefore, the reasons for missing a deer at 500 yards will likely have more to do with improperly accounted for deterministic variables and/or poor shot execution.
The conclusion to be made about hit probability in hunting situations is very similar to the conclusion made in the last chapter on score shooting. Improving the ballistic performance of your equipment can increase the margin of error for a given shooting objective, but success is very dependent on the ability of the shooter to judge wind and execute well placed shots.
The stated objective of this book is to promote successful long range shooting by establishing a strong understanding of external ballistics. Part of understanding external ballistics is knowing its relative importance in the big picture. Successful long range shooting does require a working knowledge of external ballistics, but there’s much more to it than that. If you’re serious about achieving success at any long range shooting objective, it’s important to have a well rounded understanding of all the aspects related to your chosen shooting objective including the ballistics, special skills required to handle the elements present like keeping your scope from fogging in cold weather or preventing the grease from freezing in the firing pin spring and causing a misfire. You also have to know your body and its effects on your shooting objective. How fast can you calm your heartbeat if you have to stop hiking and settle in for a long range shot? Do you have a plan for keeping the sweat from running in your eyes and compromising the sight picture? You need to have a basic understanding of the instruments you use to measure all the variables in the field. You should know the effects of moisture and temperature on the performance of your rangefinder. You need to make sure you have your weather reading instrument calibrated so you’re getting accurate measurements of temperature, humidity and pressure.
Successful long range shooting is dependent on so many things. Again, external ballistics is an important subject to study because it can help you make decisions about the best equipment for your application and allow you to make accurate corrections to your sights in order to hit targets. Keep in mind there are many other subjects that are equally critical to successful long range shooting, and don’t think you can do it all just because you read this book.
The final example in this chapter will be a little more humbling than the first. We’ll consider the effects of the non-deterministic variables involved in taking a shot at the same deer sized target at 1000 yards.
We’ll consider the ballistics of a 7mm Remington Magnum with the heavy 180 grain Berger VLD hunting bullet at an average 3000 fps muzzle velocity, with a standard deviation of 10 fps.
According to the lethality charts in the previous chapter, a large capacity 7mm cartridge with these bullets is lethal on 150 lb game up to 1225 yards, and up to 850 yards on 300 lb game. Considering the size of an average deer to be around 225-250 lb, this combination of rifle and bullet should be lethal on this game at 1000 yards. The rifle is a typical hunting rifle, capable of 1” groups at 100 yards. The times of flight for this bullet are 0.1024 seconds and 1.3157 seconds at 100 and 1000 yards, respectively. That means the smallest groups we can expect at 1000 yards are: 1 inch times 1.3157/0.1024 = 12.9 inches. Over 1000 yards, the wind will be harder to judge than over a short range, possibly blowing with different speed and direction at several points between the shooter and target. We’ll assume +/- 4 mph of crosswind uncertainty for this example. I’ll skip the component build up this time and go straight to the impact zone probability contour.
The top of Figure 15.3 shows the size and shape of the impact zone and the probability rings. As you can see, the innermost ring is about 15.4” wide and 5” tall. That’s already bigger than the vital area of the deer and there’s only a 67% chance of hitting in that ring! The bottom half of Figure 15.3 shows the 99% ring which is 46” wide and over 15” tall. Remember that this picture is for a rifle/bullet combo that has way above average ballistics and is meant for long range shooting. If the rifle were a .308 Winchester with 168 grain bullets, the impact zone would be much larger. Even with the terrific ballistic performance of the 7mm Remington Magnum with super high BC bullets and relatively low variation in both muzzle velocity and wind uncertainty, there’s still a good chance you miss will the deer completely or hit it in a non vital area, wounding the animal.
Also remember that this analysis assumes that all of the deterministic variables are completely and accurately accounted for. At this range, if the sights are canted by 5 degrees, the entire impact area will be shifted over 21” to the side! There’s also over 5” of spin drift, and don’t even think about shooting from a less than a rock solid supported position.
Publisher's Note: The book can be purchased at the LRH Gear Shop
I’m not presenting these sobering facts about the realities of long range hunting to discourage you from trying it, but to illustrate the need for complete attention to detail. If the loads for the 7mm Remington Magnum were refined a little more to reduce the muzzle velocity variation and improve the accuracy; shots were only taken in no wind or very low wind scenarios; all of the other deterministic variables were perfectly measured and accounted for; and the shot perfectly executed, it is possible to hit deer sized targets at 1000 yards on the first shot. However, you had better know what you’re doing, and put in the time on the range practicing and learning about all the variables if you expect to make successful shots on game at 1000 yards. It is possible, but it’s not a stunt and you shouldn’t risk making a shot that might wound the animal if it’s beyond the range you’ve practiced at and are comfortable shooting.
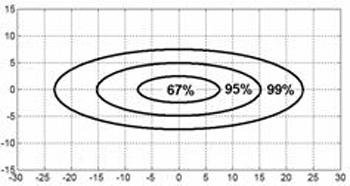

Figure 15.3. Impact area under only the influence of the non-deterministic variables.
Bryan Litz majored in Aerospace Engineering at Penn State University and worked on air-to-air missile design for 6 years in the US Air Force before taking a job as Berger Bullets Chief Ballistician in November 2008. Bryan is now 29 years old, and has been an avid long range shooter since the age of 15. In particular, Bryan enjoys NRA Long Range Prone Fullbore/Palma competition and is the current National Palma Champion. Bryan is also a husband and proud father of 3.
By Bryan Litz
The previous chapter presented a model for the lethality of hunting bullets which is one of the limiting factors in long range hunting. This chapter focuses on the other major constraint which is accuracy. Once you’ve determined the approximate maximum lethal range of your selected rifle and bullet, it’s important to understand the uncertainties involved which may cause you to miss your aimpoint. Accuracy is obviously a very important factor in long range hunting. Not only do you have to hit the animal, but you have to hit it in a vital area which is a small percentage of the animal’s total size. If you are accurate enough and can reliably place shots within the small vital area of your target, you can effectively increase the lethal range with superior shot placement
To view a 3 minute video synopsis of the book by the author CLICK HERE AND THEN PAGE DOWN
This chapter will focus on a general model that will attempt to quantify the probability of a hit against a certain target given unique field variables. For example, if you know your rifle’s inherent precision (grouping ability), muzzle velocity variation, wind uncertainty, range to target and target size, you should be able to estimate the probability of successfully hitting the target on the first shot. Like the previous chapter on lethality, the goal here is not to give hard numbers that are 100% accurate. Rather the goal is to reveal the underlying trends and provide some realistic guidance to the decision making process.Accounting for uncertainty
Long range shooting has many variables. Most of the variables can be measured and accounted for. These are known as deterministic variables. Examples of deterministic variables are: gravity drop, range, atmospherics, rifle cant (tilt), and spin drift. Every deterministic variable can be quantified and corrected for. If all variables were deterministic, shooters would only be limited by their rifles inherent precision (grouping ability). For example, if a rifle was capable of 10” groups at 1000 yards, you could expect to be able to reliably hit a 10” target at 1000 yards, etc. Long range shooters know that in reality, you cannot count on perfect shot placement. The reason why you can’t is because of the non-deterministic variables involved in long range shooting. Non-deterministic variables are those variables that cannot be measured precisely or calculated for each shot.
The two biggest non-deterministic variables remaining in long range shooting are wind determination and muzzle velocity variation. Furthermore, there are the effects introduced by firing from a cold bore.
The following analysis will proceed with the assumption that the shooter has measured and accounted for all of the deterministic variables, and will focus on the effects of the non-deterministic variables.
Figure 15.1 illustrates how the non-deterministic effects of muzzle velocity variation and wind deflection combine to shape a likely impact zone for a given set of non-deterministic variables. The goal is to determine the size and shape of the impact zone under the influence of some non-deterministic variables.
Step 1: Establish the baseline.
This is the inherent precision ability of the rifle and can be determined by averaging groups at short range. It’s important to be honest with this part. The goal is to represent the average grouping potential of the rifle, not the best ever 3 shot group. A good way to establish the baseline is to average 5 groups of 5 shots each. This will give a good representation of the rifles inherent precision. Contrary to the belief of many gun writers and shooters, a single 3-shot group is worthless for determining the grouping potential of any rifle.
For this example, we’ll consider a 30-06 rifle shooting 185 grain bullets at an average muzzle velocity of 2850 fps. The rifle will be modeled as being capable of 1” groups at 100 yards on average. For this current analysis, we’ll consider the impact zone at 500 yards. According to the principles of bullet dispersion given in Chapter 11, we can extrapolate the group size from 100 yards to 500 yards based on the bullets time of flight. The bullets time of flight at 100 yards is 0.1084 seconds, and at 500 yards, it’s 0.6154 seconds. Since the rifle is capable of grouping into 1 inch at 100 yards, we can expect the dispersion to produce a 500 yard group of: 1 inch times 0.6154/0.1084 = 5.7 inches minimum.
The next piece of information we need is the extreme spread of muzzle velocity variation for the load under consideration. The extreme spread (ES) should be mesured for as many shots as possible; at least 10 shots should make up the sample. Alternatively, you can use 4 times the standard deviation as a representation of the muzzle velocity extreme spread (+/- 2 standard deviations represents 95% confidence limits). This statistical data gathered on the muzzle velocity will be used to characterize the uncertainty of this non-deterministic variable so that we can correlate it to an expected vertical dispersion. For this example, we’ll use an extreme spread of 60 fps in muzzle velocity. That would roughly correlate to a standard deviation of about 15 fps.
Publisher's Note: The book can be purchased at the LRH Gear Shop
The final piece of information we need for step 1 is the uncertainty of the crosswind, similar to the target shooting analysis in the previous section. This is a difficult variable to nail down because it’s purely an estimate of your ability to judge the average crosswind speed between you and the target. How accurately this can be done depends on the indicators that are available, the complexity of the wind patterns present, and the accuracy of the individual’s estimations. You can get an idea of how accurate your wind estimation is by taking a wind meter into the field, guessing at the wind speed, and seeing how close you come to the measured wind speed. This exercise will also serve as a learning experience, allowing you to calibrate your observations into accurate wind speeds. You will need to make a guess as to what your ability is to estimate crosswind speed in mph. For this example, we’ll say the shooter is capable of estimating crosswind within +/- 2 mph.So the raw parameters we’ll be using to create the impact zone analysis at 500 yards are:
• Rifle capable of averaging 1” groups at 100 yards: extrapolates to 5.7 inches minimum at 500 yards.
• 60 fps extreme spread in muzzle velocity
• +/- 2 mph uncertainty in crosswind speed
The rifle’s inherent precision and the extreme spread of muzzle velocity can be considered relatively constant values whereas the uncertainty in wind speed is something that could be different for each shot.
Step 2: Turn the raw uncertainties into inches of deflection at the target range.
This can easily be done with the included software. We’ll do the vertical plane first. Using all of the pertinent variables, calculate the drop at 500 yards for the average muzzle velocity. The 185 grain bullets at 2850 fps will have about 49” of drop at 500 yards from a 100 yard zero. Now add ½ of the extreme spread to the muzzle velocity to see what the difference in drop is. An additional 30 fps in muzzle velocity would cause a round to hit about 1.2” higher at 500 yards, so you can expect +/- 1.2”, or 2.4” of vertical spread in addition to the 5.7” inherent precision of the rifle at 500 yards.
Now here comes a little twist. In order to quantify the total vertical dispersion, you can’t simply add the 5.7” and 2.4”. The likely magnitude of multiple random errors is quantified using the RSS method which stands for Root Sum Squares. Mathematically, the sum is written as:
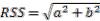
Where a and b are the two components being added. In this case, the total likely vertical dispersion is:
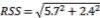
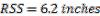
So the likely total vertical dispersion from the rifles inherent precision and the velocity variation is 6.2” total.
Now let’s consider the horizontal plane.
We have estimated +/- 2 mph of crosswind uncertainty for this example. Again, using the ballistics program, convert this wind uncertainty to inches of deflection for the pertinent variables. In this case, a 2 mph crosswind will result in +/- 3.1” of wind deflection at 500 yards, a total horizontal error of 6.2”. The RSS of the horizontal components of dispersion yields:
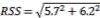
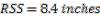
So the likely total horizontal dispersion is +/- 4.2 inches, or 8.4 inches total at 500 yards with the non-deterministic variables we’re using in this example. This information is best represented visually. Refer to Figure 15.1 for an illustration of the expected cumulative dispersion.
Notice how the muzzle velocity variation adds some uncertainty to the vertical shape of the group, and the wind uncertainty adds some uncertainty to the horizontal shape. The probability contour in the bottom right corner of Figure 15.1 shows the regions and associated probability of impacts. For example, there is a 67% chance the rounds will strike the inner ring (2.1 inches tall by 2.8 inches wide), a 95% chance that the rounds will strike in the next biggest ring (4.1 inches tall and 5.6 inches wide), and a 99% chance the rounds will strike in the largest ring (6.2 inches tall by 8.4 inches wide).
Publisher's Note: The book can be purchased at the LRH Gear Shop

Figure 15.1. Cumulative effects of non-deterministic variables on a 500 yard target.
It’s very important to remember that this analysis assumes that all of the deterministic variables are accounted for. If the rifle is slightly canted, spin drift unaccounted for, shot taken from a poorly supported position, sights not properly calibrated and adjusted, zero not accurately set, etc etc, the impact zone will be the same size, but it will not be centered on the aim point which will likely result in a miss. Figure 15.2 shows the likely impact zone from the previous example and its relative size on the vital area of a deer; as well as the effects of having an unaccounted for deterministic variable.
To view a 3 minute video synopsis of the book by the author CLICK HERE AND THEN PAGE DOWN
As illustrated in Figure 15.2, if all the deterministic variables are accounted for, then the uncertainty introduced by the muzzle velocity variation and wind uncertainty isn’t enough to cause a miss on a typical white tailed deer at 500 yards (left). However, if the deterministic variables are not perfectly accounted for, the impact zone can be offset from the aim point and result in a miss. The example in Figure 15.2 has the impact zone shifted by about 15 inches. At 500 yards, if the rifle is canted by just 5 degrees, it will cause the point of impact to shift laterally by 4.3 inches in this example. In contrast, spin drift is only worth about 1.4 inches at this range. The most likely cause of offsetting the aim point in a hunting situation is the combination of not having a perfectly steady platform to shoot from, and being excited about the shot. These real world effects can easily compromise shot placement as much as any other variable.

Figure 15.2. If all of the deterministic variables are accounted for, the impact zone will be centered on the aim point. However if the deterministic variables are unaccounted for the impact zone will be offset and a miss can result.
In the above analysis, the ballistic performance of the rifle/bullet comes into play in the step where you translate the non-deterministic variables into physical displacement on the target. The better the ballistic performance of your bullets, the less wind deflection you will incur from a given uncertainty of crosswind speed. Seeing as how wind is usually the greatest non-deterministic variable, ballistic performance turns out to play quite an important role in the size of the expected impact zone. Furthermore, improved inherent precision of the rifle and more consistent muzzle velocities will serve to further shrink the size of the expected impact zone. However, taking another look at Figure 15.2 for the 500 yard shot on a deer, it’s clear that the impact zone is small enough to insure a pretty reliable hit on a deer sized target. Therefore, the reasons for missing a deer at 500 yards will likely have more to do with improperly accounted for deterministic variables and/or poor shot execution.
The conclusion to be made about hit probability in hunting situations is very similar to the conclusion made in the last chapter on score shooting. Improving the ballistic performance of your equipment can increase the margin of error for a given shooting objective, but success is very dependent on the ability of the shooter to judge wind and execute well placed shots.
The stated objective of this book is to promote successful long range shooting by establishing a strong understanding of external ballistics. Part of understanding external ballistics is knowing its relative importance in the big picture. Successful long range shooting does require a working knowledge of external ballistics, but there’s much more to it than that. If you’re serious about achieving success at any long range shooting objective, it’s important to have a well rounded understanding of all the aspects related to your chosen shooting objective including the ballistics, special skills required to handle the elements present like keeping your scope from fogging in cold weather or preventing the grease from freezing in the firing pin spring and causing a misfire. You also have to know your body and its effects on your shooting objective. How fast can you calm your heartbeat if you have to stop hiking and settle in for a long range shot? Do you have a plan for keeping the sweat from running in your eyes and compromising the sight picture? You need to have a basic understanding of the instruments you use to measure all the variables in the field. You should know the effects of moisture and temperature on the performance of your rangefinder. You need to make sure you have your weather reading instrument calibrated so you’re getting accurate measurements of temperature, humidity and pressure.
Successful long range shooting is dependent on so many things. Again, external ballistics is an important subject to study because it can help you make decisions about the best equipment for your application and allow you to make accurate corrections to your sights in order to hit targets. Keep in mind there are many other subjects that are equally critical to successful long range shooting, and don’t think you can do it all just because you read this book.
The final example in this chapter will be a little more humbling than the first. We’ll consider the effects of the non-deterministic variables involved in taking a shot at the same deer sized target at 1000 yards.
We’ll consider the ballistics of a 7mm Remington Magnum with the heavy 180 grain Berger VLD hunting bullet at an average 3000 fps muzzle velocity, with a standard deviation of 10 fps.
According to the lethality charts in the previous chapter, a large capacity 7mm cartridge with these bullets is lethal on 150 lb game up to 1225 yards, and up to 850 yards on 300 lb game. Considering the size of an average deer to be around 225-250 lb, this combination of rifle and bullet should be lethal on this game at 1000 yards. The rifle is a typical hunting rifle, capable of 1” groups at 100 yards. The times of flight for this bullet are 0.1024 seconds and 1.3157 seconds at 100 and 1000 yards, respectively. That means the smallest groups we can expect at 1000 yards are: 1 inch times 1.3157/0.1024 = 12.9 inches. Over 1000 yards, the wind will be harder to judge than over a short range, possibly blowing with different speed and direction at several points between the shooter and target. We’ll assume +/- 4 mph of crosswind uncertainty for this example. I’ll skip the component build up this time and go straight to the impact zone probability contour.
The top of Figure 15.3 shows the size and shape of the impact zone and the probability rings. As you can see, the innermost ring is about 15.4” wide and 5” tall. That’s already bigger than the vital area of the deer and there’s only a 67% chance of hitting in that ring! The bottom half of Figure 15.3 shows the 99% ring which is 46” wide and over 15” tall. Remember that this picture is for a rifle/bullet combo that has way above average ballistics and is meant for long range shooting. If the rifle were a .308 Winchester with 168 grain bullets, the impact zone would be much larger. Even with the terrific ballistic performance of the 7mm Remington Magnum with super high BC bullets and relatively low variation in both muzzle velocity and wind uncertainty, there’s still a good chance you miss will the deer completely or hit it in a non vital area, wounding the animal.
Also remember that this analysis assumes that all of the deterministic variables are completely and accurately accounted for. At this range, if the sights are canted by 5 degrees, the entire impact area will be shifted over 21” to the side! There’s also over 5” of spin drift, and don’t even think about shooting from a less than a rock solid supported position.
Publisher's Note: The book can be purchased at the LRH Gear Shop
I’m not presenting these sobering facts about the realities of long range hunting to discourage you from trying it, but to illustrate the need for complete attention to detail. If the loads for the 7mm Remington Magnum were refined a little more to reduce the muzzle velocity variation and improve the accuracy; shots were only taken in no wind or very low wind scenarios; all of the other deterministic variables were perfectly measured and accounted for; and the shot perfectly executed, it is possible to hit deer sized targets at 1000 yards on the first shot. However, you had better know what you’re doing, and put in the time on the range practicing and learning about all the variables if you expect to make successful shots on game at 1000 yards. It is possible, but it’s not a stunt and you shouldn’t risk making a shot that might wound the animal if it’s beyond the range you’ve practiced at and are comfortable shooting.


Figure 15.3. Impact area under only the influence of the non-deterministic variables.
Bryan Litz majored in Aerospace Engineering at Penn State University and worked on air-to-air missile design for 6 years in the US Air Force before taking a job as Berger Bullets Chief Ballistician in November 2008. Bryan is now 29 years old, and has been an avid long range shooter since the age of 15. In particular, Bryan enjoys NRA Long Range Prone Fullbore/Palma competition and is the current National Palma Champion. Bryan is also a husband and proud father of 3.

