ken snyder
Well-Known Member
- Joined
- Jul 26, 2010
- Messages
- 420
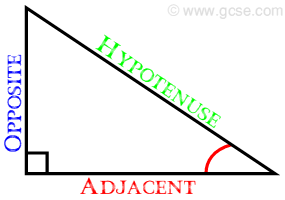
So here I am on the side of a steep slope, it is 900 yds. down to target level and the target is 900 yds. in front of me. The bullet I am useing goes subsonic at 1,050 yrds. my conclusion is that the target is 222yds. out of range for me. Whats your conclusion?