Measuring Barrel Friction In The 5.56mm NATO
By Patrick Boyle, Alexander Humphrey, Spencer Proctor, and Michael Courtney
U.S. Air Force Academy, 2354 Fairchild Drive, USAF Academy, CO 80840
[email protected]
©Copyright Precision Shooting Magazine
Abstract
The 5.56mm NATO cartridge is used by the United States Armed Forces and the Armed Forces of other NATO Nations. Despite its wide use, current methods for finding the barrel friction of the bullet are not accurate or consistent. This paper presents a new method for finding this barrel friction by analyzing the linear muzzle energy vs. powder charge found by test firing 5.56mm NATO round with different powder weights. When graphing the relationship between the energy vs. powder charge (Alliant Blue Dot Powder) of the Nosler 40 grain ballistic tip lead free, Hornady 53 grain VMAX, and the Hornady 60 grain VMAX bullets it was noticed that the relationship was near-perfectly linear. This allows for the barrel friction of these rounds to be calculated by finding the vertical intercept on the graph of the muzzle energy vs. powder charge which represents the work done by friction in foot pounds. When the work of friction is divided by barrel length in feet, the barrel friction in pounds is found with an uncertainty near 3% for the jacketed lead bullets and 6.4% for the lead free bullet design. The new method of measuring barrel friction is expected to provide a quantitative way to compare the friction (or reduced friction) of differing bullet designs, barrel materials, bullet coatings, and polishing methods.
Introduction
The 5.56mm NATO round is widely used throughout the United States and NATO Armed Forces (Colt 2003). Because of its wide use, it is important to know the barrel friction. High barrel friction robs bullets of energy that could otherwise be used to incapacitate the target, penetrate intermediate barriers, resist wind drift, or flatten trajectories. Also, high friction can contribute to the barrel overheating, which can affect the barrel integrity, life, and accuracy. At any given limit on cartridge pressure, bullets with lower friction can be fired with higher muzzle velocity, because the pressure has less friction to overcome and will provide greater acceleration to the bullet. In the context of a bullet moving in a rifle barrel, there are a number of forces resisting forward motion, and the present study focuses on the total work needed to overcome the net resisting force including the forces needed to engrave the bullet and the forces needed to overcome friction.
One method for estimating barrel friction is to analyze the pressure curve that is created when shots are fired. This method’s accuracy can be influenced by several confounding factors including the mass of the powder, the spatial variation in pressure between the point of measurement and the base of the bullet, shot-to-shot variations in the pressure curve, and gas blow by. A second method uses a guess of the friction as an input for numerical modeling and adjusts the guess until agreement is found with the measured pressure curve and velocity. Since the pressure curve and velocity might be subject to other factors, this method provides only an estimate. A third method is to measure the force required to push bullets through the bore with a rod at low speeds, 1.3 and 3.6 inches per second (White and Siewert 2007). This method has the advantage of providing a complete force curve: the barrel resistance at every position as the bullet moves down the barrel. However, it is not clear how well this might represent resistance forces in the barrel at the much higher velocities involved in firing or whether this method accurately simulates the effects of powder or copper fouling of the barrel. A second limitation of that study was that only the resistance forces in the first 4 inches of the barrel were measured, so the barrel friction in the complete barrel was undetermined. The method presented here is less subject to the confounding factors of the first two methods, so it offers greater potential for accuracy. The method of the present study also determines the average resistant force at ballistic velocities and because it is based on live firing, it also incorporates real effects of copper and powder fouling in the barrel.
Method
The velocity of various bullets was measured with an optical chronograph (Oehler 35 with accuracy estimated at 0.3%) as the powder charge of Alliant Blue Dot powder was varied in 1 grain steps from 5 or 6 grains up to 14 grains. All loads used Federal 205M primers. The resulting velocity is combined with bullet mass to compute muzzle energy in foot pounds. When the energy in foot pounds is graphed as a function of the amount of powder in grains, the resulting graph illustrates a strong linear relationship with a coefficient of determination (R2) above 0.997. This relationship can therefore be used to calculate the work done by friction on the bullet (in foot pounds) by the vertical intercept, which is the energy lost to friction. The average frictional force can then be calculated by taking the lost energy (vertical intercept) and dividing by the barrel length (1.875 feet for the Remington 700 chambered in .223 Rem used here).
The specific bullets tested were the Nosler 40 grain ballistic tip lead free (Nosler, Bend OR, Part # 45160), Hornady 53 grain VMAX (Hornady, Grand Island, NE, Part # 22265), and the Hornady 60 grain VMAX (Hornady, Grand Island, NE, Part # 22281). Using the velocities in feet per second found with the chronograph and an Excel spreadsheet, one is able to calculate the muzzle energy in foot pounds for each shot. For each bullet and powder charge, the muzzle energy was averaged for five shots. A linear regression of muzzle energy vs. powder charge yields the slope which is the additional energy for each additional grain of powder and the vertical intercept which is the energy lost to friction of each bullet. To calculate the average frictional force, the energy lost to friction (in foot-pounds) is divided by the barrel length (in feet) to yield the force of friction (in pounds).
Results
For the powder and charge weights employed here, the relationship between muzzle energy and powder charge had a very high linear correlation (R2 > 0.997). The constant efficiency over a broad range of powder charges allows extrapolation back to the vertical intercept to provide a determination of the energy lost to barrel friction. Table 1 provides the work of friction and average force of friction for each bullet. The work of friction is found by interpreting the vertical intercepts of these graphs to indicate the amount of energy necessary for the bullet to leave the barrel. The uncertainty of friction ranges from near 3% for the jacketed lead bullets to 6.4% for the lead free design.
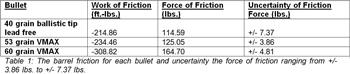
Figure 1 shows the relationship between the powder in grains and the muzzle energy in ft-lbs of the Nosler 40 grain ballistic tip lead free. The vertical intercept of this graph shows that it requires 214.86 ft-lbs of energy for the bullet to exit the barrel. The average force of friction over the length of the barrel is 114.59 lbs. With Blue Dot powder, the Nosler 40 grain ballistic tip lead free has a slope of 77.50 ft-lbs per grain which represents the average increase in muzzle energy for each additional grain of powder.
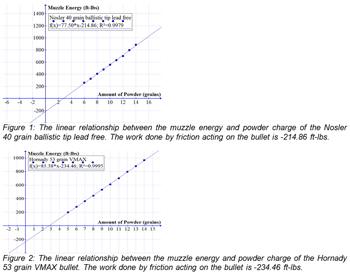
Figure 2 shows the relationship between the powder in grains and the muzzle energy in ft-lbs of the Hornady 53 grain VMAX bullet. The vertical intercept of this graph shows that it requires 234.46 ft-lbs of energy for the bullet to exit the barrel. The force of friction, which is the average friction over the length of the barrel, is 125.05 lbs. Hornady 53 grain VMAX bullet has a slope of 85.38 ft-lbs per grain which represents the average increase in muzzle energy for each additional grain of powder.
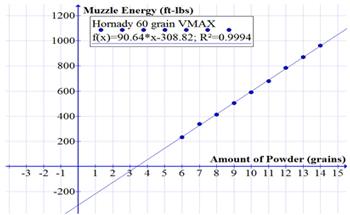
Figure 3 shows the relationship between the powder in grains and the muzzle energy in ft-lbs of the Hornady 60 grain VMAX bullet. The vertical intercept of this graph shows that it requires 308.82 ft-lbs of energy for the bullet to exit the barrel. The force of friction, which is the average friction over the length of the barrel, is 164.70 lbs. The Hornady 60 grain VMAX bullet has a slope of 90.64 ft-lbs per grain which represents the average increase in muzzle energy for each additional grain of powder.
Discussion
Limitations
This method only works when using certain powders that have a linear relationship of muzzle energy vs. powder charge so that powder efficiency and work done by friction can be determined as the slope and vertical intercept of a regression line. If another powder were used, there is some likelihood that the relationship between the powder charge and muzzle energy would not be linear. This method provides an accurate way to measure the average muzzle energy per grain of powder when analyzing the slope of a line for each bullet. Once one has established that the powder being used has a linear relationship, one can use this method to find the work done by friction for the bullet.
It should be noted that many powders can seem to give a linear energy vs. powder charge over a small range, but are unsuitable for estimating barrel friction unless they allow confident extrapolation back to the vertical intercept. Figure 4 shows an energy vs. powder charge graph generated with QuickLOAD V3.6 for H4895 powder and the 60 grain VMAX. (QuickLOAD is an internal ballistics modeling program that predicts muzzle velocities from powder and bullet properties.) At first glance, the data seems linear, and can be fit with a linear function giving a very high R2 of over 0.99. However, more careful analysis reveals a distinct upward curvature of the data, and a quadratic function provides a much better fit. Since the derivative of the energy vs. powder charge curve is not exactly constant, it is not possible to reliably extrapolate back to the vertical intercept to estimate barrel friction by using this powder. In a limited number of cases, QuickLOAD seems to reliably indicate which powders have a sufficiently linear response over a large range of charge weights to confidently extrapolate back to the vertical intercept to determine barrel friction. Some powders (like H4895) gain efficiency as the powder charge is increased. Other powders (usually those with slower burn rates) show diminishing returns as additional powder is added because the powder has not completely burned and the pressure is still high as the bullet leaves the barrel.
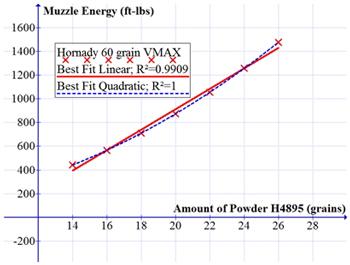
Figure 4: Muzzle energy vs. powder charge as predicted by QuickLOAD V3.6 for H4895 and the 60 grain Hornady VMAX bullet, along with the best fit linear and quadratic functions.
Further Study: Testing Claims of Reduced Friction
The results of this experiment provide an accurate, quantitative method for measuring the average barrel friction of the 5.56mm NATO cartridge with various bullets. In addition, it provides a method for testing manufacturer’s claims for reducing barrel friction, such as Norma’s moly bullets (Norma 2011) and SMOOTH-KOTE barrel liner (SMOOTH-KOTE 2006) by comparing the resulting frictions found between treated and untreated barrels and bullets. Bore Tech claims that its drive band technology reduces pressure and fouling thus providing higher velocities for the same bullet weight (Bore Tech 2007). Several patents make claims regarding the friction reducing effects of molybdenum disulfide and tungsten disulfide (Martin 2000) as well as for a proprietary oxide coating using the trade name Lubalox (Stock and Eberhart 2007). The Martin patent (2000) claims that the plating process described allows an increase of bullet velocity by 10%, which would require over a 50% reduction in barrel friction. The authors of the present study are unaware of any published data quantifying these friction reducing claims.
Further Study: Friction of Military Bullets
Analysis of a smaller sample size of velocity data from a separate experiment (armor testing) with the same rifle and the M193 and M855 bullets suggests that while the full metal jacketed M193 bullet had friction comparable with the other 5.56mm bullets at 222 ft-lbs (+/- 21 ft-lbs) of energy lost to friction, the M855 bullet had much larger friction at 412 ft-lbs (+/- 42 ft-lbs) of energy lost to barrel friction. The larger uncertainties are due to the smaller sample sizes and the sealant between the bullet and cartridge case that produces larger shot-to-shot variations in bullet velocity with a given powder charge. The larger friction of the M855 is consistent with the trend of barrel friction increasing with bullet mass, probably attributable to an increase in bearing surface of the longer bullets, but other factors in bullet construction may also contribute. In light of the fact that reducing friction by 50% has the potential to add 200 ft-lbs to the muzzle energy for such a friction prone bullet design, it would seem prudent in the future to understand and mitigate the barrel friction of bullets adopted for military use.
Further Study: Increased Friction Caused by Lead Free Primers
Analysis of a smaller sample size of velocity data from a separate experiment (lead free primers) with the same rifle and lead free bullets suggests a large (>90%) increase in friction when using lead free rather than lead styphnate based primers. Dave Summer, a chemist at the United States Air Force Academy, has suggested (private communication) that the residual lead might be increasing lubricity and that switching to lead free primers might have unintended consequences analogous to engine performance difficulties associated with the switch to lead free gasoline. The impact of lead styphnate vs. lead free primers on friction should be carefully quantified in addition to satisfying previously enumerated criteria (Courtney and Courtney 2011) to ensure a smooth transition to the new technology.
Acknowledgements
This research was funded by BTG Research (www.btgresearch.org). The authors are grateful for the use of the range owned by Louisiana Shooters Unlimited to collect data. We are also appreciative of the valuable range assistance of Elya Courtney. Dave Summer (USAFA/DFRL) and Lt Col Scott Callihan (USAFA/DFMS) read the manuscript and offered many helpful comments.
Bibliography
"Barrel Treatment with SMOOTH-KOTE and/or BP2000." Smooth-KOTE. 2006. Sentry Solutions. 17 Oct. 2011. < http://www.sentrysolutions.com/mm5/merchant.mvc?Screen=APL03 >.
"Bore Tech V3 Precision Match" Boretech.com. 2007. 19 Oct. 2011. /www.boretech.com/products/bulletsv3.shtml>.
"Comparing Blast Pressure Variations of Lead Styphnate Based and Diazodinitrophenol Based Primers", Amy Courtney and Michael Courtney. 2011. The WSTIAC Journal. Volume 11. Number 2. < http://wstiac.alionscience.com/pdf/WQV11N2_ART01.pdf >
"Final Report of the Rifling Profile Push Test", 2007. Lin White and Jeff Siewert, ARL-CR-593, http://www.dtic.mil/dtic/tr/fulltext/u2/a469801.pdf .
"M16A4 5.56mm Rifle" Colt.com. 2003. Colt. 22 Oct. 2011.
/web.archive.org/web/20110616205850/http://www.colt.com/mil/M16.asp >
"Method of Impact Plating a Bullet With a Powdered Lubricant", Martin M.D., US Patent 6036996. 2000.
"Norma Diamond Line." Norma.com. 2011. Norma 10 Oct. 2011. /www.norma.cc/en/Products/Our-Brands/Norma-Diamond-Line/ >.
"Upset Jacketed Bullets", Stock M.E., Eberhart G.T., US Patent 2007/0131131 A1. 2007.
By Patrick Boyle, Alexander Humphrey, Spencer Proctor, and Michael Courtney
U.S. Air Force Academy, 2354 Fairchild Drive, USAF Academy, CO 80840
[email protected]
©Copyright Precision Shooting Magazine
Abstract
The 5.56mm NATO cartridge is used by the United States Armed Forces and the Armed Forces of other NATO Nations. Despite its wide use, current methods for finding the barrel friction of the bullet are not accurate or consistent. This paper presents a new method for finding this barrel friction by analyzing the linear muzzle energy vs. powder charge found by test firing 5.56mm NATO round with different powder weights. When graphing the relationship between the energy vs. powder charge (Alliant Blue Dot Powder) of the Nosler 40 grain ballistic tip lead free, Hornady 53 grain VMAX, and the Hornady 60 grain VMAX bullets it was noticed that the relationship was near-perfectly linear. This allows for the barrel friction of these rounds to be calculated by finding the vertical intercept on the graph of the muzzle energy vs. powder charge which represents the work done by friction in foot pounds. When the work of friction is divided by barrel length in feet, the barrel friction in pounds is found with an uncertainty near 3% for the jacketed lead bullets and 6.4% for the lead free bullet design. The new method of measuring barrel friction is expected to provide a quantitative way to compare the friction (or reduced friction) of differing bullet designs, barrel materials, bullet coatings, and polishing methods.
Introduction
The 5.56mm NATO round is widely used throughout the United States and NATO Armed Forces (Colt 2003). Because of its wide use, it is important to know the barrel friction. High barrel friction robs bullets of energy that could otherwise be used to incapacitate the target, penetrate intermediate barriers, resist wind drift, or flatten trajectories. Also, high friction can contribute to the barrel overheating, which can affect the barrel integrity, life, and accuracy. At any given limit on cartridge pressure, bullets with lower friction can be fired with higher muzzle velocity, because the pressure has less friction to overcome and will provide greater acceleration to the bullet. In the context of a bullet moving in a rifle barrel, there are a number of forces resisting forward motion, and the present study focuses on the total work needed to overcome the net resisting force including the forces needed to engrave the bullet and the forces needed to overcome friction.
One method for estimating barrel friction is to analyze the pressure curve that is created when shots are fired. This method’s accuracy can be influenced by several confounding factors including the mass of the powder, the spatial variation in pressure between the point of measurement and the base of the bullet, shot-to-shot variations in the pressure curve, and gas blow by. A second method uses a guess of the friction as an input for numerical modeling and adjusts the guess until agreement is found with the measured pressure curve and velocity. Since the pressure curve and velocity might be subject to other factors, this method provides only an estimate. A third method is to measure the force required to push bullets through the bore with a rod at low speeds, 1.3 and 3.6 inches per second (White and Siewert 2007). This method has the advantage of providing a complete force curve: the barrel resistance at every position as the bullet moves down the barrel. However, it is not clear how well this might represent resistance forces in the barrel at the much higher velocities involved in firing or whether this method accurately simulates the effects of powder or copper fouling of the barrel. A second limitation of that study was that only the resistance forces in the first 4 inches of the barrel were measured, so the barrel friction in the complete barrel was undetermined. The method presented here is less subject to the confounding factors of the first two methods, so it offers greater potential for accuracy. The method of the present study also determines the average resistant force at ballistic velocities and because it is based on live firing, it also incorporates real effects of copper and powder fouling in the barrel.
Method
The velocity of various bullets was measured with an optical chronograph (Oehler 35 with accuracy estimated at 0.3%) as the powder charge of Alliant Blue Dot powder was varied in 1 grain steps from 5 or 6 grains up to 14 grains. All loads used Federal 205M primers. The resulting velocity is combined with bullet mass to compute muzzle energy in foot pounds. When the energy in foot pounds is graphed as a function of the amount of powder in grains, the resulting graph illustrates a strong linear relationship with a coefficient of determination (R2) above 0.997. This relationship can therefore be used to calculate the work done by friction on the bullet (in foot pounds) by the vertical intercept, which is the energy lost to friction. The average frictional force can then be calculated by taking the lost energy (vertical intercept) and dividing by the barrel length (1.875 feet for the Remington 700 chambered in .223 Rem used here).
The specific bullets tested were the Nosler 40 grain ballistic tip lead free (Nosler, Bend OR, Part # 45160), Hornady 53 grain VMAX (Hornady, Grand Island, NE, Part # 22265), and the Hornady 60 grain VMAX (Hornady, Grand Island, NE, Part # 22281). Using the velocities in feet per second found with the chronograph and an Excel spreadsheet, one is able to calculate the muzzle energy in foot pounds for each shot. For each bullet and powder charge, the muzzle energy was averaged for five shots. A linear regression of muzzle energy vs. powder charge yields the slope which is the additional energy for each additional grain of powder and the vertical intercept which is the energy lost to friction of each bullet. To calculate the average frictional force, the energy lost to friction (in foot-pounds) is divided by the barrel length (in feet) to yield the force of friction (in pounds).
Results
For the powder and charge weights employed here, the relationship between muzzle energy and powder charge had a very high linear correlation (R2 > 0.997). The constant efficiency over a broad range of powder charges allows extrapolation back to the vertical intercept to provide a determination of the energy lost to barrel friction. Table 1 provides the work of friction and average force of friction for each bullet. The work of friction is found by interpreting the vertical intercepts of these graphs to indicate the amount of energy necessary for the bullet to leave the barrel. The uncertainty of friction ranges from near 3% for the jacketed lead bullets to 6.4% for the lead free design.

Figure 1 shows the relationship between the powder in grains and the muzzle energy in ft-lbs of the Nosler 40 grain ballistic tip lead free. The vertical intercept of this graph shows that it requires 214.86 ft-lbs of energy for the bullet to exit the barrel. The average force of friction over the length of the barrel is 114.59 lbs. With Blue Dot powder, the Nosler 40 grain ballistic tip lead free has a slope of 77.50 ft-lbs per grain which represents the average increase in muzzle energy for each additional grain of powder.

Figure 2 shows the relationship between the powder in grains and the muzzle energy in ft-lbs of the Hornady 53 grain VMAX bullet. The vertical intercept of this graph shows that it requires 234.46 ft-lbs of energy for the bullet to exit the barrel. The force of friction, which is the average friction over the length of the barrel, is 125.05 lbs. Hornady 53 grain VMAX bullet has a slope of 85.38 ft-lbs per grain which represents the average increase in muzzle energy for each additional grain of powder.

Figure 3 shows the relationship between the powder in grains and the muzzle energy in ft-lbs of the Hornady 60 grain VMAX bullet. The vertical intercept of this graph shows that it requires 308.82 ft-lbs of energy for the bullet to exit the barrel. The force of friction, which is the average friction over the length of the barrel, is 164.70 lbs. The Hornady 60 grain VMAX bullet has a slope of 90.64 ft-lbs per grain which represents the average increase in muzzle energy for each additional grain of powder.
Discussion
Limitations
This method only works when using certain powders that have a linear relationship of muzzle energy vs. powder charge so that powder efficiency and work done by friction can be determined as the slope and vertical intercept of a regression line. If another powder were used, there is some likelihood that the relationship between the powder charge and muzzle energy would not be linear. This method provides an accurate way to measure the average muzzle energy per grain of powder when analyzing the slope of a line for each bullet. Once one has established that the powder being used has a linear relationship, one can use this method to find the work done by friction for the bullet.
It should be noted that many powders can seem to give a linear energy vs. powder charge over a small range, but are unsuitable for estimating barrel friction unless they allow confident extrapolation back to the vertical intercept. Figure 4 shows an energy vs. powder charge graph generated with QuickLOAD V3.6 for H4895 powder and the 60 grain VMAX. (QuickLOAD is an internal ballistics modeling program that predicts muzzle velocities from powder and bullet properties.) At first glance, the data seems linear, and can be fit with a linear function giving a very high R2 of over 0.99. However, more careful analysis reveals a distinct upward curvature of the data, and a quadratic function provides a much better fit. Since the derivative of the energy vs. powder charge curve is not exactly constant, it is not possible to reliably extrapolate back to the vertical intercept to estimate barrel friction by using this powder. In a limited number of cases, QuickLOAD seems to reliably indicate which powders have a sufficiently linear response over a large range of charge weights to confidently extrapolate back to the vertical intercept to determine barrel friction. Some powders (like H4895) gain efficiency as the powder charge is increased. Other powders (usually those with slower burn rates) show diminishing returns as additional powder is added because the powder has not completely burned and the pressure is still high as the bullet leaves the barrel.

Figure 4: Muzzle energy vs. powder charge as predicted by QuickLOAD V3.6 for H4895 and the 60 grain Hornady VMAX bullet, along with the best fit linear and quadratic functions.
Further Study: Testing Claims of Reduced Friction
The results of this experiment provide an accurate, quantitative method for measuring the average barrel friction of the 5.56mm NATO cartridge with various bullets. In addition, it provides a method for testing manufacturer’s claims for reducing barrel friction, such as Norma’s moly bullets (Norma 2011) and SMOOTH-KOTE barrel liner (SMOOTH-KOTE 2006) by comparing the resulting frictions found between treated and untreated barrels and bullets. Bore Tech claims that its drive band technology reduces pressure and fouling thus providing higher velocities for the same bullet weight (Bore Tech 2007). Several patents make claims regarding the friction reducing effects of molybdenum disulfide and tungsten disulfide (Martin 2000) as well as for a proprietary oxide coating using the trade name Lubalox (Stock and Eberhart 2007). The Martin patent (2000) claims that the plating process described allows an increase of bullet velocity by 10%, which would require over a 50% reduction in barrel friction. The authors of the present study are unaware of any published data quantifying these friction reducing claims.
Further Study: Friction of Military Bullets
Analysis of a smaller sample size of velocity data from a separate experiment (armor testing) with the same rifle and the M193 and M855 bullets suggests that while the full metal jacketed M193 bullet had friction comparable with the other 5.56mm bullets at 222 ft-lbs (+/- 21 ft-lbs) of energy lost to friction, the M855 bullet had much larger friction at 412 ft-lbs (+/- 42 ft-lbs) of energy lost to barrel friction. The larger uncertainties are due to the smaller sample sizes and the sealant between the bullet and cartridge case that produces larger shot-to-shot variations in bullet velocity with a given powder charge. The larger friction of the M855 is consistent with the trend of barrel friction increasing with bullet mass, probably attributable to an increase in bearing surface of the longer bullets, but other factors in bullet construction may also contribute. In light of the fact that reducing friction by 50% has the potential to add 200 ft-lbs to the muzzle energy for such a friction prone bullet design, it would seem prudent in the future to understand and mitigate the barrel friction of bullets adopted for military use.
Further Study: Increased Friction Caused by Lead Free Primers
Analysis of a smaller sample size of velocity data from a separate experiment (lead free primers) with the same rifle and lead free bullets suggests a large (>90%) increase in friction when using lead free rather than lead styphnate based primers. Dave Summer, a chemist at the United States Air Force Academy, has suggested (private communication) that the residual lead might be increasing lubricity and that switching to lead free primers might have unintended consequences analogous to engine performance difficulties associated with the switch to lead free gasoline. The impact of lead styphnate vs. lead free primers on friction should be carefully quantified in addition to satisfying previously enumerated criteria (Courtney and Courtney 2011) to ensure a smooth transition to the new technology.
Acknowledgements
This research was funded by BTG Research (www.btgresearch.org). The authors are grateful for the use of the range owned by Louisiana Shooters Unlimited to collect data. We are also appreciative of the valuable range assistance of Elya Courtney. Dave Summer (USAFA/DFRL) and Lt Col Scott Callihan (USAFA/DFMS) read the manuscript and offered many helpful comments.
Bibliography
"Barrel Treatment with SMOOTH-KOTE and/or BP2000." Smooth-KOTE. 2006. Sentry Solutions. 17 Oct. 2011. < http://www.sentrysolutions.com/mm5/merchant.mvc?Screen=APL03 >.
"Bore Tech V3 Precision Match" Boretech.com. 2007. 19 Oct. 2011. /www.boretech.com/products/bulletsv3.shtml>.
"Comparing Blast Pressure Variations of Lead Styphnate Based and Diazodinitrophenol Based Primers", Amy Courtney and Michael Courtney. 2011. The WSTIAC Journal. Volume 11. Number 2. < http://wstiac.alionscience.com/pdf/WQV11N2_ART01.pdf >
"Final Report of the Rifling Profile Push Test", 2007. Lin White and Jeff Siewert, ARL-CR-593, http://www.dtic.mil/dtic/tr/fulltext/u2/a469801.pdf .
"M16A4 5.56mm Rifle" Colt.com. 2003. Colt. 22 Oct. 2011.
/web.archive.org/web/20110616205850/http://www.colt.com/mil/M16.asp >
"Method of Impact Plating a Bullet With a Powdered Lubricant", Martin M.D., US Patent 6036996. 2000.
"Norma Diamond Line." Norma.com. 2011. Norma 10 Oct. 2011. /www.norma.cc/en/Products/Our-Brands/Norma-Diamond-Line/ >.
"Upset Jacketed Bullets", Stock M.E., Eberhart G.T., US Patent 2007/0131131 A1. 2007.

