A Scientific Basis for Evaluating Variable Crosswinds
By Paul Carter
Although we frequently discuss wind as if it is constant in both magnitude and direction, that’s seldom true in the real shooting world, where features of terrain make accurate wind doping much more challenging. For instance, it’s possible that a significant wind experienced at the shooter’s location may be completely blocked somewhere downrange by a hill or other physical entity. Of course, the converse can be true, also. In that event, the bullet’s flight could be influenced by a wind which is present closer to the target but absent at the shooting location.
An interesting and practical wind-doping problem arises regarding the previously mentioned wind-blocked-by-hill scenarios. Specifically, when considering the amount of wind drift that must be corrected for, does it make any difference when the bullet experiences wind? In other words, is the bullet exposed to wind early in flight deflected more than, less than or the same amount as a bullet which starts its journey under calm conditions but is exposed to wind near the end of its flight?
In order to investigate this matter, let’s establish some conditions. The range will be 1,000 yards and we’ll be dealing with a 10-mph crosswind from 9 o’clock. In the first instance (Wind Early), we’ll assume this wind is present for the first half of the bullet’s journey (0-500 yards). Thereafter, the wind will be completely blocked. In the second scenario (Wind Late), the wind will be blocked until the bullet reaches the 500-yard mark. For the second half of its flight (500-1,000 yards) the bullet will be exposed to the crosswind.
At first glance, it might seem reasonable to assume that wind drift under both conditions would be equal. After all, the same bullet is exposed to a wind of the same strength and direction over the exact same distance. Unfortunately, it’s not that simple! There are additional factors at play. Chief among them is the scientific concept of momentum. Once an object (bullet) is acted upon by a force (in this case the wind) and put into motion, it tends to stay in motion unless acted upon by another force. Sir Isaac Newton said it best: “A body at rest tends to stay at rest; a body in motion tends to stay in motion.” When a bullet encounters a crosswind upon exiting the muzzle, that wind will cause the bullet to drift as long as the wind is acting upon the projectile. However, even if the wind’s influence is subsequently removed, the bullet will continue to move laterally, resulting in additional drift by the time it reaches the target.
To better illustrate this phenomenon consider a boat with a motor at a lake. The boat starts from a stationary position. Once the engine is running the boat begins to move in a particular direction. If the motor is turned off the boat does not come to an immediate stop. Instead, it continues to drift in the direction of travel. How far the boat travels is largely a function of the boat’s speed and the frictional force exerted on the boat by the water which surrounds it. For a bullet in flight, the wind fulfills the same role as the boat motor, while the atmosphere replaces water as the medium of travel.
Returning to our 1,000-yard shooting experiment, let’s do some calculations and see what conclusions can be drawn. For a baseline, let’s start by calculating the expected bullet drift for a thousand-yard shot, where a 10-mph crosswind is acting upon the bullet over the entire range. We’ll be shooting a 185 grain Berger VLD bullet (B.C. = .569) out of a .300 Winchester magnum at a muzzle velocity of 2,865 feet per second. In order to calculate the drift, we’ll need the time it takes for the bullet to travel 1,000 yards and an appropriate formula. From the Sierra Infinity ballistic software (Version 6), we find that the time of flight to travel 1,000 yards is 1.4376 seconds. A formula which describes the deflection of a bullet in a crosswind has been developed. In the absence of a headwind for a level-fire scenario, this formula is:
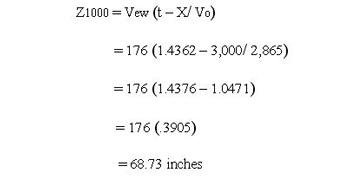
Where Z is the cross-range deflection in inches,
Vew is the cross-range wind velocity in inches/ second (1 mph = 17.60 inches/ second),
t is the bullet’s true time of flight in seconds,
X in the range to the target in feet, and
Vo is the muzzle velocity of the bullet in feet/ second.
Plugging the relevant values into the equation 1, we get:

If we use the Infinity software to check our math, we find the exact same prediction of bullet drift for a 1,000-yard shot in the presence of a constant 10-mph wind. Obviously, bullet drift for both the Wind Early and the Wind Late scenarios will necessarily be less than this.
In order to find the drift values for the Wind Early and Wind Late circumstances, we’ll have to alter the approach somewhat. These situations, as well as all others where the wind speed and/or direction is not constant along the entire range to target, fall into a different category, appropriately described as variable crosswinds. The approximate effect of a variable crosswind can be determined by analyzing the problem as a series of constant crosswinds acting over short intervals, each of which starts at a different down-range distance from the gun muzzle. The Wind Early scenario is comprised of two wind segments: 10 mph over the first 500-yard interval and 0 mph over the second 500-yard interval; for the Wind Late situation, the segments are the same but the wind speeds are reversed. For a variable wind comprised of more than one segment, the following formula can be used to calculate the drift for each segment:

Equation 2 is really a variation of equation 1, allowing for the calculation of the drift observed at the target range [Z(R)] resulting from a particular wind acting during an interval of bullet flight beginning at some point downrange (a) and ending at a point further downrange (b). The symbols Xa and Xb represent the starting and ending ranges of the interval (feet); t(Xa) and t(Xb) refer to the bullet’s time of flight to reach each of those ranges (seconds); and Vxa and Vxb are the down-range velocities (feet/ second) of the bullet when it reaches those ranges. The symbol R represents the range to target (feet) and t(R) is the time of flight to the target (seconds).
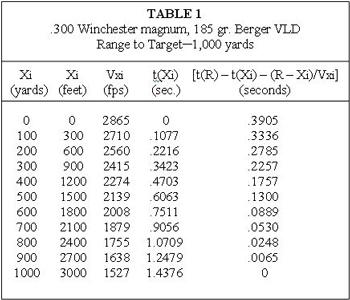
Table 1 shows the values of these variables, in 100-yard increments, for the present study. The flight times and bullet velocities were taken from Sierra’s Infinity software. The fifth column represents the calculated numerical value (seconds) of the bracketed portion of equation 2 at various ranges. To find the bullet drift attributable to a particular wind, the numerical value in column 5 which corresponds with the range where the wind interval ends is subtracted from the value corresponding to the range where the wind interval begins. The resulting quantity is then multiplied by the applicable wind velocity (inches/ second) to give the drift.
To start, let’s use Table 1 to calculate the drift for the Wind Early case. Of course, the first wind segment begins at the muzzle and ends at 500 yards. The wind velocity for this interval of flight is 10 mph (176 inches/ second). Therefore, the drift attributable to this segment can be calculated by:

It’s important to note that this figure represents the drift, attributed to this particular wind segment, which will be observed at 1,000 yards (target distance). Since the wind velocity is zero for the second segment of flight, there is no additional contribution to bullet drift. However, if a crosswind was present for the second segment, then that would obviously impact the total amount of drift. The same process would be employed to calculate the drift caused by a second-segment wind. The total drift would be determined by simply adding the drift caused by the two wind segments. Any additional wind segments would be analyzed in a similar fashion, with the total drift comprising the sum of the drift calculated for the individual segments.
The remaining task is to calculate the drift for the Wind Late scenario. From the previous discussion, we know that drift from the first wind segment is zero because the wind velocity is zero for the first 500 yards of flight. The drift from 500-1000 yards, and therefore the total drift, can be calculated by:
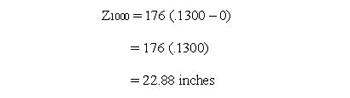
Now that our calculations are complete, what conclusions can be drawn? First, as it relates to drift experienced at the target, it’s apparent that bullets are much more sensitive to wind near the muzzle than they are to the same wind near the target. Actually, for this particular set of circumstances, the early wind caused approximately twice the drift of an equivalent late wind. Second, when the drift seen in the Wind Early scenario is added to that observed in the Wind Late scenario, the result (68.73 inches) corresponds exactly to the independent calculation we performed for a constant 10-mph crosswind acting over the entire 1,000-yard range. Since the net effect of combining the Wind Early and Wind Late cases results in a constant 10-mph crosswind across the full 1,000-yard range, logic dictates that total bullet drift be the same also.
The key finding is that approximately two-thirds (45.85/68.73) of the total drift seen at 1,000 yards for a constant 10-mph crosswind is attributable to the first 500 yards of bullet flight, while only about one-third is caused by the second half of flight. This has practical implications for the long-range shooter. Most of us carry a data card or some other means of referencing important ballistic data, so we can make corrections for range, shooting angle and wind. Usually, drift data for a constant 10-mph crosswind is referenced. When faced with a variable wind the aforementioned information can help us make the proper adjustment.
As an example, consider the following hypothetical situation: While hunting mule deer you glass a nice buck, which you subsequently range at 800 yards. For a shot of this length in the presence of a constant 10-mph crosswind, your data card predicts 41 inches of drift. As you evaluate the wind, however, you’re confident you’re dealing with a 10-mph crosswind at your shooting position but you’re just as sure there’s little wind near the target. If you feel the wind is steady until about halfway to the buck (400 yards), then you can be comfortable correcting for two-thirds of the drift listed on the data card, which amounts to 27 inches (41 x ⅔ = 27.33). If you determine that the wind is a factor for only the first 300 yards, using 50% of the listed drift (20.5 inches) would be a good approximation; if you feel the wind maintains its gusto to the 500-yard mark, then correcting for 75% of the 800-yard drift (31 inches) might be appropriate.
This presentation provides a true scientific rationale for correcting for bullet drift in variable crosswinds. I’ve demonstrated the relevant mathematical formulas and calculations as a means of proving the validity of my statements. However, an appreciation of the practical effects of wind on a bullet is much more important than being able to manipulate formulas. Towards that end, the only thing that needs to be remembered is the ⅔-⅓ rule. That is: in the presence of a constant crosswind, approximately two-thirds of the drift seen at the target is caused during the first half of bullet flight, while the remaining one-third of the total drift results from the second half of the bullet’s journey.
Armed with this information, the long-range practitioner can make more accurate corrections in shooting situations where variable crosswinds are present. Version 6 of the Sierra Infinity ballistic software has the ability to calculate total bullet drift for scenarios consisting of a maximum of five separate wind segments. This capability can be used to sharpen one’s wind-compensation skills. Hypothetical wind problems, featuring wind segments of varying lengths, wind speeds and directions, can be evaluated using one’s data card, common sense and the information discussed here. Once a prediction of total bullet drift at the target has been estimated, it can be compared to the precise formulation produced by the software program. Over time, these exercises will pay dividends when a shot really counts.
References: McCoy, Robert L., Modern Exterior Ballistics, Schiffer Publishing Ltd.,
Atglen, Pennsylvania, 1999
“Crosswinds,” www.exteriorballistics.com/ebexplained/4th/532.cfm
©Copyright 2011 by Paul C. Carter
Paul C. Carter is a big-game hunter and author who resides in Massachusetts. He has hunted game across North America, taking numerous animals, many with a muzzle-loading rifle. He especially enjoys hunting sheep and whitetail deer. Paul has two Grand Slams of North American wild sheep to his credit, one of which was taken with his iron-sighted muzzleloader. He’s also written two books: Tracking Whitetails: Answers to Your Questions and Great Shot! A Guide to Acquiring Shooting Skills for Big-Game Hunters.
By Paul Carter
Although we frequently discuss wind as if it is constant in both magnitude and direction, that’s seldom true in the real shooting world, where features of terrain make accurate wind doping much more challenging. For instance, it’s possible that a significant wind experienced at the shooter’s location may be completely blocked somewhere downrange by a hill or other physical entity. Of course, the converse can be true, also. In that event, the bullet’s flight could be influenced by a wind which is present closer to the target but absent at the shooting location.
An interesting and practical wind-doping problem arises regarding the previously mentioned wind-blocked-by-hill scenarios. Specifically, when considering the amount of wind drift that must be corrected for, does it make any difference when the bullet experiences wind? In other words, is the bullet exposed to wind early in flight deflected more than, less than or the same amount as a bullet which starts its journey under calm conditions but is exposed to wind near the end of its flight?
In order to investigate this matter, let’s establish some conditions. The range will be 1,000 yards and we’ll be dealing with a 10-mph crosswind from 9 o’clock. In the first instance (Wind Early), we’ll assume this wind is present for the first half of the bullet’s journey (0-500 yards). Thereafter, the wind will be completely blocked. In the second scenario (Wind Late), the wind will be blocked until the bullet reaches the 500-yard mark. For the second half of its flight (500-1,000 yards) the bullet will be exposed to the crosswind.
At first glance, it might seem reasonable to assume that wind drift under both conditions would be equal. After all, the same bullet is exposed to a wind of the same strength and direction over the exact same distance. Unfortunately, it’s not that simple! There are additional factors at play. Chief among them is the scientific concept of momentum. Once an object (bullet) is acted upon by a force (in this case the wind) and put into motion, it tends to stay in motion unless acted upon by another force. Sir Isaac Newton said it best: “A body at rest tends to stay at rest; a body in motion tends to stay in motion.” When a bullet encounters a crosswind upon exiting the muzzle, that wind will cause the bullet to drift as long as the wind is acting upon the projectile. However, even if the wind’s influence is subsequently removed, the bullet will continue to move laterally, resulting in additional drift by the time it reaches the target.
To better illustrate this phenomenon consider a boat with a motor at a lake. The boat starts from a stationary position. Once the engine is running the boat begins to move in a particular direction. If the motor is turned off the boat does not come to an immediate stop. Instead, it continues to drift in the direction of travel. How far the boat travels is largely a function of the boat’s speed and the frictional force exerted on the boat by the water which surrounds it. For a bullet in flight, the wind fulfills the same role as the boat motor, while the atmosphere replaces water as the medium of travel.
Returning to our 1,000-yard shooting experiment, let’s do some calculations and see what conclusions can be drawn. For a baseline, let’s start by calculating the expected bullet drift for a thousand-yard shot, where a 10-mph crosswind is acting upon the bullet over the entire range. We’ll be shooting a 185 grain Berger VLD bullet (B.C. = .569) out of a .300 Winchester magnum at a muzzle velocity of 2,865 feet per second. In order to calculate the drift, we’ll need the time it takes for the bullet to travel 1,000 yards and an appropriate formula. From the Sierra Infinity ballistic software (Version 6), we find that the time of flight to travel 1,000 yards is 1.4376 seconds. A formula which describes the deflection of a bullet in a crosswind has been developed. In the absence of a headwind for a level-fire scenario, this formula is:
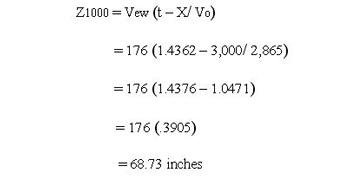
Where Z is the cross-range deflection in inches,
Vew is the cross-range wind velocity in inches/ second (1 mph = 17.60 inches/ second),
t is the bullet’s true time of flight in seconds,
X in the range to the target in feet, and
Vo is the muzzle velocity of the bullet in feet/ second.
Plugging the relevant values into the equation 1, we get:

If we use the Infinity software to check our math, we find the exact same prediction of bullet drift for a 1,000-yard shot in the presence of a constant 10-mph wind. Obviously, bullet drift for both the Wind Early and the Wind Late scenarios will necessarily be less than this.
In order to find the drift values for the Wind Early and Wind Late circumstances, we’ll have to alter the approach somewhat. These situations, as well as all others where the wind speed and/or direction is not constant along the entire range to target, fall into a different category, appropriately described as variable crosswinds. The approximate effect of a variable crosswind can be determined by analyzing the problem as a series of constant crosswinds acting over short intervals, each of which starts at a different down-range distance from the gun muzzle. The Wind Early scenario is comprised of two wind segments: 10 mph over the first 500-yard interval and 0 mph over the second 500-yard interval; for the Wind Late situation, the segments are the same but the wind speeds are reversed. For a variable wind comprised of more than one segment, the following formula can be used to calculate the drift for each segment:

Equation 2 is really a variation of equation 1, allowing for the calculation of the drift observed at the target range [Z(R)] resulting from a particular wind acting during an interval of bullet flight beginning at some point downrange (a) and ending at a point further downrange (b). The symbols Xa and Xb represent the starting and ending ranges of the interval (feet); t(Xa) and t(Xb) refer to the bullet’s time of flight to reach each of those ranges (seconds); and Vxa and Vxb are the down-range velocities (feet/ second) of the bullet when it reaches those ranges. The symbol R represents the range to target (feet) and t(R) is the time of flight to the target (seconds).
Table 1 shows the values of these variables, in 100-yard increments, for the present study. The flight times and bullet velocities were taken from Sierra’s Infinity software. The fifth column represents the calculated numerical value (seconds) of the bracketed portion of equation 2 at various ranges. To find the bullet drift attributable to a particular wind, the numerical value in column 5 which corresponds with the range where the wind interval ends is subtracted from the value corresponding to the range where the wind interval begins. The resulting quantity is then multiplied by the applicable wind velocity (inches/ second) to give the drift.

To start, let’s use Table 1 to calculate the drift for the Wind Early case. Of course, the first wind segment begins at the muzzle and ends at 500 yards. The wind velocity for this interval of flight is 10 mph (176 inches/ second). Therefore, the drift attributable to this segment can be calculated by:

It’s important to note that this figure represents the drift, attributed to this particular wind segment, which will be observed at 1,000 yards (target distance). Since the wind velocity is zero for the second segment of flight, there is no additional contribution to bullet drift. However, if a crosswind was present for the second segment, then that would obviously impact the total amount of drift. The same process would be employed to calculate the drift caused by a second-segment wind. The total drift would be determined by simply adding the drift caused by the two wind segments. Any additional wind segments would be analyzed in a similar fashion, with the total drift comprising the sum of the drift calculated for the individual segments.
The remaining task is to calculate the drift for the Wind Late scenario. From the previous discussion, we know that drift from the first wind segment is zero because the wind velocity is zero for the first 500 yards of flight. The drift from 500-1000 yards, and therefore the total drift, can be calculated by:
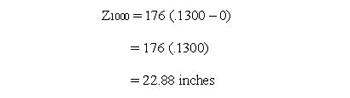
Now that our calculations are complete, what conclusions can be drawn? First, as it relates to drift experienced at the target, it’s apparent that bullets are much more sensitive to wind near the muzzle than they are to the same wind near the target. Actually, for this particular set of circumstances, the early wind caused approximately twice the drift of an equivalent late wind. Second, when the drift seen in the Wind Early scenario is added to that observed in the Wind Late scenario, the result (68.73 inches) corresponds exactly to the independent calculation we performed for a constant 10-mph crosswind acting over the entire 1,000-yard range. Since the net effect of combining the Wind Early and Wind Late cases results in a constant 10-mph crosswind across the full 1,000-yard range, logic dictates that total bullet drift be the same also.
The key finding is that approximately two-thirds (45.85/68.73) of the total drift seen at 1,000 yards for a constant 10-mph crosswind is attributable to the first 500 yards of bullet flight, while only about one-third is caused by the second half of flight. This has practical implications for the long-range shooter. Most of us carry a data card or some other means of referencing important ballistic data, so we can make corrections for range, shooting angle and wind. Usually, drift data for a constant 10-mph crosswind is referenced. When faced with a variable wind the aforementioned information can help us make the proper adjustment.
As an example, consider the following hypothetical situation: While hunting mule deer you glass a nice buck, which you subsequently range at 800 yards. For a shot of this length in the presence of a constant 10-mph crosswind, your data card predicts 41 inches of drift. As you evaluate the wind, however, you’re confident you’re dealing with a 10-mph crosswind at your shooting position but you’re just as sure there’s little wind near the target. If you feel the wind is steady until about halfway to the buck (400 yards), then you can be comfortable correcting for two-thirds of the drift listed on the data card, which amounts to 27 inches (41 x ⅔ = 27.33). If you determine that the wind is a factor for only the first 300 yards, using 50% of the listed drift (20.5 inches) would be a good approximation; if you feel the wind maintains its gusto to the 500-yard mark, then correcting for 75% of the 800-yard drift (31 inches) might be appropriate.
This presentation provides a true scientific rationale for correcting for bullet drift in variable crosswinds. I’ve demonstrated the relevant mathematical formulas and calculations as a means of proving the validity of my statements. However, an appreciation of the practical effects of wind on a bullet is much more important than being able to manipulate formulas. Towards that end, the only thing that needs to be remembered is the ⅔-⅓ rule. That is: in the presence of a constant crosswind, approximately two-thirds of the drift seen at the target is caused during the first half of bullet flight, while the remaining one-third of the total drift results from the second half of the bullet’s journey.
Armed with this information, the long-range practitioner can make more accurate corrections in shooting situations where variable crosswinds are present. Version 6 of the Sierra Infinity ballistic software has the ability to calculate total bullet drift for scenarios consisting of a maximum of five separate wind segments. This capability can be used to sharpen one’s wind-compensation skills. Hypothetical wind problems, featuring wind segments of varying lengths, wind speeds and directions, can be evaluated using one’s data card, common sense and the information discussed here. Once a prediction of total bullet drift at the target has been estimated, it can be compared to the precise formulation produced by the software program. Over time, these exercises will pay dividends when a shot really counts.
References: McCoy, Robert L., Modern Exterior Ballistics, Schiffer Publishing Ltd.,
Atglen, Pennsylvania, 1999
“Crosswinds,” www.exteriorballistics.com/ebexplained/4th/532.cfm
©Copyright 2011 by Paul C. Carter
Paul C. Carter is a big-game hunter and author who resides in Massachusetts. He has hunted game across North America, taking numerous animals, many with a muzzle-loading rifle. He especially enjoys hunting sheep and whitetail deer. Paul has two Grand Slams of North American wild sheep to his credit, one of which was taken with his iron-sighted muzzleloader. He’s also written two books: Tracking Whitetails: Answers to Your Questions and Great Shot! A Guide to Acquiring Shooting Skills for Big-Game Hunters.

