Stability: Fine Points to be Aware Of

[nralifer]

Bullet stability is fundamental to not only accuracy but also to effective deep penetration. A marginally stable bullet mey group well at 100 yds but start to tumble at 300. Also, bullets are less stable at sea level than at 5000 ft, BECAUSE AT SEA LEVEL THE AIR DENSITY THEY ARE TRAVELING IN IS HIGHER THAN AT 5000 FT. Likewise, when a bullet enters an animal the density of the medium it is traveling in SUDDENLY INCREASES well beyond the air it traveled through to get there. To achieve as straight a line of penetration as possible and adequate bullet expansion, the bullet must be traveling nose forward and not tumbling. The barrel twist rate and muzzle velocity impart to the bullet the rotational speed (RPM) that determines the stability. This rotational speed is entirely separate from its forward speed (FPS). This latter speed degrades much more quickly than the rotational speed as it is a function of the bullet BC whereas the rotational speed is not, for all practical considerations. It is the rotational speed measured as RPMs, that determines the stability of the bullet through air AND the target medium, whether that be tissue or ballistic gel.

The following is an illustration of the effect MV has on rotational speed of a bullet. Consider a 30 cal bullet shot through a 1:10 twist barrel first at 1700 fps an then at 3000 fps. At 1700 fps the bullet leaves the barrel rotating at 122,400 rpm. At 3000 fps the bullet rotational speed is now 216,000 rpm, a difference of 93,600 rpm. In air over a short distance the slower bullet may be stable enough to hit nose foreward, but as it enters a much denser medium (10% gel for instance) it will start to tumble almost immediately and not expand properly. Not only that, but the path the tumbling bullet will follow is much more erratic. Proper gel testing of bullet expansion demands that the bullet, in its trek through the gel, be spinning at a high enough RPM to keep it traveling nose forward.

These principles also apply to subsonic loads. They require a tighter twist barrel to impart the proper RPMs to the bullet to keep it stable over several hundreds of yards.

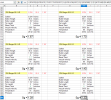
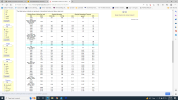
The following pictures show a .284 160 gr BD2 expansion at reduced muzzle velocities. All were shot from a 1:7 twist barrel.

 

[Mikecr]

There are a couple errors in this (perspective-wise).

1. A bullet that groups at all at 100yds will not hit a tumbling concern again until transonic. This, because gyroscopic stability increases as a bullet travels down range, all the way to transonic. The biggest free flight destabilizing moment is muzzle release. This is why bullets that will tumble generally do so immediately (within 10yds). They don't just decide to tumble on their own later.

2. Gyroscopic stability has nothing to do with RPMs. Stability requirements are not expressed in turns per time, but displacement per turn. Displacement being air density, and turns being imparted by rifling twist.
So an 8:1 twist requirement is 8" of a standard air density, per 1 turn, to gyroscopically overcome the overturning drag in that 8".
Doesn't matter the velocity, or resultant turns per time. You need one turn per every 8", and this is set by twist.

I understand that you're going at this from a terminal ballistic standpoint, but you cannot muddle these things in external ballistics to do it.

 

[nralifer]

There are a couple errors in this (perspective-wise).

1. A bullet that groups at all at 100yds will not hit a tumbling concern again until transonic. This, because gyroscopic stability increases as a bullet travels down range, all the way to transonic. The biggest free flight destabilizing moment is muzzle release. This is why bullets that will tumble generally do so immediately (within 10yds). They don't just decide to tumble on their own later.

2. Gyroscopic stability has nothing to do with RPMs. Stability requirements are not expressed in turns per time, but displacement per turn. Displacement being air density, and turns being imparted by rifling twist.
So an 8:1 twist requirement is 8" of a standard air density, per 1 turn, to gyroscopically overcome the overturning drag in that 8".
Doesn't matter the velocity, or resultant turns per time. You need one turn per every 8", and this is set by twist.

I understand that you're going at this from a terminal ballistic standpoint, but you cannot muddle these things in external ballistics to do it.

Beg to differ. Early pn we made a 320 gr .338 that from a 1:9 twist at 100 yds at 60 degrees grouped one hole for 5 shots. Later in the winter at 5 degrees we shot the same bullet to 500 yds and every hit was sideways. Clearly the air was denser and there was a progressive tumbling that developed as the bullet traveled down range. It is the spin of the bullet that gives it its gyroscopic stability and long bullets have to be spun faster to maintain stability. Discussed the issue with some ballistisian from Hornady who said that was impossible, yet we obsrved it plain as day. If you take the JBM Stability Calculator and progressively increase the atmospheric pressure in the calculator you will see that the stability factor decreases. Do the opposite and it increases. Inadequately stabilized bullets will definitely tumble in gel if marginally stable in air. Why do you suppose subsonic bullets need tighter twists to stabilize? Gyroscopes become more stable the faster you spin them, and as they lose angular momentum they become more unstable. The basic gyroscopic principle is that a spining gyroscope resists torquing forces perpendicular to the spin axis. Bullets shot from rifled barrels have spin axes collinear with the direction of flight.

 

[tim_w]

.........Crap I edited and removed all of my post. Grr

.............Ok had most of it saved .

Your test is flawed.

You shot a bullet at 100 yd in 60F and it grouped well. You then shot the same bullet at the same location in 5F temps @ 500 yd and it key holed.

Thos only proves that the same load and bullet in denser air had lower SG. It proves nothing about a bullet having the decreased stability as it travels down range. SG only improves with time downrange.


Further, you did not also shoot the 5F test at 100yd which would have in all likelihood also been keyholing. I assume it was the same load as you were trying to compare apples to apples. Issue is most all gunpowder loses MV as temp drops and certainly going from 60F to 5F. Significant changes when you get well below freezing.

For your claim to disprove bullets become less stable downrange you would have had to shoot the same bullet in the same gun/barrel at both 100 yd and then 500 yds. The 100yd would punch round holes small group and the 500 yd target would have oblong or keyholes.


If you were trying to prove the air density increase was the cause, you could have shot at the same location at the same distance. One in warm temps the other in very cold temps but you would need to be doing it over a chrono to show that both loads had the same MV.


BTW all of this has been well proven using very tightly controlled scientific methods. This has been known for a century. In more recent times using doplar radar to track the entire bullet path. Their numerous results conflict directly with your statement that bullets during super sonic flight become less stable over time as the forward velocity decreases. It's been proven that a bullets forward velocity decays at a faster rate than its rotational velocity (rpms).

Further you run into the difference in gyroscopic stability and dynamic stability. The latter can be effected by bullet design.

Then you have the effects of higher SG on drag model as it traverses flesh. Of the effects on bullet path thru flesh the least effect is gyro stability within the normal range in rifles and bullets. Bullet sectional density and design/construction has far greater effects.

If you want to put forward support for your claim that refutes the generally accepted performance by the community then please post up studies or statements from authoritative individuals who conducted tightly controlled studies. Fact is a bullets SG increases over time. This happens because vel decays at a faster rate than rotational decay. Think where the greatest focus of air pressure is on a bullet in flight. It's not on the side of the bullet body with perpendicular focus it's on the tip in a focused cone opposing the direction of flight.

This is not touching on bullet design effects o dynamic stability as it crosses into traditional Mach vel such as the mach1.2-0.8 transsonic range. Look at the history of the 30 cal 168 SMK for how a bullet can have plenty of gyroscopic stability SG 1.5+ at MV but because of its design still falls apart as it enters this vel range. Compare it to a Berger 168 gr same SG at MV which will not fall apart as it drops out of solid mach1+ vel.

As for subsonic ammo such as the 300 BO/whisper. Most of the MV are in the teansonic range which is the worst window for bullet exit. Mach 0.8-0.9 or 895-1000 fps. Further bullet designed for super sonic flight have differing stability ranges. Bullets designed specifically for subsonic have weight forward designs. If you look at the rpm to vel ratio of a typical super sonic bullet when it reaches subsonic vel it will have a SG far greater and in the range or greater than what's achieved with these faster twist barrels fired at subsonic vel. What it comes down to is bullet design transitional vel windows from Mach 1 to sub vel. You also have the effects of the powders used and the powder volumes are far from ideal for precision. Shoot subsonic in a normal case volune with slower powders and you see a significant improvement in precision. 308 case 220 bullet 850 fps MV 9 tw.

 

[Mikecr]

Beg to differ. Early pn we made a 320 gr .338 that from a 1:9 twist at 100 yds at 60 degrees grouped one hole for 5 shots. Later in the winter at 5 degrees we shot the same bullet to 500 yds and every hit was sideways. Clearly the air was denser and there was a progressive tumbling that developed as the bullet traveled down range.

When a bullet travels downrange it's forward velocity slows more than it's turning velocity. So a bullet muzzle released at 9:1, can have a relative 7:1 twist rate by 500yds. If you run the numbers on that you see that Sg at 7:1 is significantly higher. Sg should be considerably higher by 500yds.
Your bullet did not begin as stable and destabilize from initial gyroscopic stability. Nor did the bullets fly sideways out to 500yds.

What can happen is that your bullets were dynamically unstable to a point where gyroscopic forces could not gain control.
The bullets were never gyroscopically stable. Maybe from jacket failure, or poor bullet design.
This is rare, an anomaly, and not normal. I think only the 168smk is known to have a dynamic instability due to design.

Anyway, any air density departing from standard represents a displacement in ratio to standard.
An air density twice as high is relatively twice the displacement to set turns.
So yeah, Sg is directly tied to air density.
Again, nothing to do with RPMs, as changing RPMs is not changing displacement per turn.
And that 7:1 500yd relative Sg is not due to higher RPMs (the RPMs are lower at 500yds).

You can round about correlate RPMs with results. But if you try to predict results, using RPMs, you will fail.
It would be little different than trying to predict BC from RPMs (using similar correlations).
Drag and stability loosely follow each other, so it might be suggested that drag and RPMs follow each other.
No,, they don't.

OOPS, typing same time as Tim_W

 

[tim_w]

Yep I thought the same thing when I refreshed my page. Lol

Then I went to change some typos and deleted my entire post.!! Was going to just leave it as you covered the same but I had a older version in my clip board. But I had to edit a bunch. Grrrr.


I recall in the early 2k when all kinds of stuff was being thrown out there. Bullet patents etc Back in the 90s people were scratching their heads on the 30 cal 168 SMKs falling apart past 600 yd. All kinds of theories.

Then the long debates on message boards rss e5c about yaw and nose angle vs bullet trajectory. Then we got doplar radar plots and eyes were opened.

 

[Hugnot]

The Miller Sg estimator:





The Berger Stability Calculator:





Altitude & Barometric Pressure:






Running my home-made spreadsheet using the Miller method & comparing the Sg estimates with the Berger stability analysis for the Berger 85.5 .224 bullet, 7.7 twist, 3050 fps, 89 deg, 0 sea level, I produced a Sg of 1.43 with my home-made number fixer & the Berger Sg analyst stuff produced a Sg of 1.42. Berger than stated the Sg of 1.42 was "marginal".

Going into this the gyroscopic effect:

"Gyroscopic motion is the tendency of a rotating object to maintain the orientation of its rotation. A rotating object possesses angular momentum and this momentum must be conserved. The object will resist any change in its axis of rotation, as a change in orientation will result in a change in angular momentum."

In addition - precession - coning motion:

"Torque-induced precession (gyroscopic precession) is the phenomenon in which the axis of a spinning object (e.g., a gyroscope) describes a cone in space when an external torque is applied to it. The phenomenon is commonly seen in a spinning toy top, but all rotating objects can undergo precession."

Like move 90 degrees from direction force applied then rotating point describes a cone.

The Miller Sg estimator process applied by my home-made Sg number fixer & the Berger Sg analyzer accepts data like twist, velocity, pressure, temp. Looking at velocity & twist: a ratio of diameter H131/ twist H135 and a comparison of velocity H136 - 2800 (a standard) is used.

The rotational stuff like RPM's would be regarded as constant over the bullet's relatively short TOF. Per Berger, factors like twist, velocity, & air density would affect stability, like lower Sg values and less than optimum performance, less than the optimum BC.

I like the Hornady 4DOF ballistic calculator, it shows Sg's increasing down range. Initial Sg's are affected by MV & twist rate. Features like aerodynamic jump & spin drift are included. "The barrel twist, velocity, and air density will determine the muzzle Sg along with other projectile properties included in the projectile file."

 

[Pdvdh]

Nice discussion.

 

[nralifer]

How do you suppose gyroscopic stability is achieved if not through turning the bullet? You need to read the explanation on the Berger web site.

 

[nralifer]

The Miller Sg estimator:

View attachment 399230



The Berger Stability Calculator:

View attachment 399228



Altitude & Barometric Pressure:

View attachment 399231




Running my home-made spreadsheet using the Miller method & comparing the Sg estimates with the Berger stability analysis for the Berger 85.5 .224 bullet, 7.7 twist, 3050 fps, 89 deg, 0 sea level, I produced a Sg of 1.43 with my home-made number fixer & the Berger Sg analyst stuff produced a Sg of 1.42. Berger than stated the Sg of 1.42 was "marginal".

Going into this the gyroscopic effect:

"Gyroscopic motion is the tendency of a rotating object to maintain the orientation of its rotation. A rotating object possesses angular momentum and this momentum must be conserved. The object will resist any change in its axis of rotation, as a change in orientation will result in a change in angular momentum."

In addition - precession - coning motion:

"Torque-induced precession (gyroscopic precession) is the phenomenon in which the axis of a spinning object (e.g., a gyroscope) describes a cone in space when an external torque is applied to it. The phenomenon is commonly seen in a spinning toy top, but all rotating objects can undergo precession."

Like move 90 degrees from direction force applied then rotating point describes a cone.

The Miller Sg estimator process applied by my home-made Sg number fixer & the Berger Sg analyzer accepts data like twist, velocity, pressure, temp. Looking at velocity & twist: a ratio of diameter H131/ twist H135 and a comparison of velocity H136 - 2800 (a standard) is used.

The rotational stuff like RPM's would be regarded as constant over the bullet's relatively short TOF. Per Berger, factors like twist, velocity, & air density would affect stability, like lower Sg values and less than optimum performance, less than the optimum BC.

I like the Hornady 4DOF ballistic calculator, it shows Sg's increasing down range. Initial Sg's are affected by MV & twist rate. Features like aerodynamic jump & spin drift are included. "The barrel twist, velocity, and air density will determine the muzzle Sg along with other projectile properties included in the projectile file."

What does barrel twist due to a bullet? It causes to spin, right? That spin rate is expressed in rpm. As you increase the number of turns in a shorter distance (barrel twist rate) inevitably the spin rate has to increase. As you increase the forward speed of the bullet for a given twist rate, the number of rotations the bullet does per unit time has to increase, thus the SG number increases as does the bullet stability. Since stability is also a function of the density of the air, decreasing as the air desity increases, one requires a faster spin rate to achieve stability. When the spining bullet suddenly enters a much denser medium, the flesh of the target animal, the bullet becomes less stable. If the bullet is marginally stable in air it will inevitably become unstable when encountering a suddenly denser medium and start to tumble. That tumbling will cause an erratic path of bullet penetration which inevitably affects terminal performance.

 

[Pdvdh]

I don't think anyone said bullet rotation wasn't a factor. But there were some additional factors brought into this discussion.

Bullet SG stability calculations are strictly a mathematical modeling effort to determine if bullets will be stable, shoot with good precision, in earth's atmosphere (air).

Bullet SG factor was never intended to predict straight line bullet penetration in a game animal. Higher SG could help straight line penetration. There's real life evidence higher SG improves the odds of straight line bullet penetration in game animals. But there are other, much larger, cause and effect factors in play after a bullet impacts a game animal.

Compare the density of air to water. Big difference. SG helps predict stable bullet flight thru air. Not thru much denser flesh and water.

 

[nralifer]

When a bullet travels downrange it's forward velocity slows more than it's turning velocity. So a bullet muzzle released at 9:1, can have a relative 7:1 twist rate by 500yds. If you run the numbers on that you see that Sg at 7:1 is significantly higher. Sg should be considerably higher by 500yds.
Your bullet did not begin as stable and destabilize from initial gyroscopic stability. Nor did the bullets fly sideways out to 500yds.

What can happen is that your bullets were dynamically unstable to a point where gyroscopic forces could not gain control.
The bullets were never gyroscopically stable. Maybe from jacket failure, or poor bullet design.
This is rare, an anomaly, and not normal. I think only the 168smk is known to have a dynamic instability due to design.

Anyway, any air density departing from standard represents a displacement in ratio to standard.
An air density twice as high is relatively twice the displacement to set turns.
So yeah, Sg is directly tied to air density.
Again, nothing to do with RPMs, as changing RPMs is not changing displacement per turn.
And that 7:1 500yd relative Sg is not due to higher RPMs (the RPMs are lower at 500yds).

You can round about correlate RPMs with results. But if you try to predict results, using RPMs, you will fail.
It would be little different than trying to predict BC from RPMs (using similar correlations).
Drag and stability loosely follow each other, so it might be suggested that drag and RPMs follow each other.
No,, they don't.

OOPS, typing same time as Tim_W

No question that from the start the stability of the bullet was low, but it was stable enough to print a tiny group at 100 yds in less dense air. My point is that initial stability is important and that one needs to achieve a high enough stability from the start so that the bullet encountering the target remains flying nose forward through the target to expand properly and have a straight enough path to perform well.

 

[nralifer]

No question that from the start the stability of the bullet was low, but it was stable enough to print a tiny group at 100 yds in less dense air. My point is that initial stability is important and that one needs to achieve a high enough stability from the start so that the bullet encountering the target remains flying nose forward through the target to expand properly and have a straight enough path to perform well.

All i can tell you is that if a bullet is marginally stable before impact it will tumble quickly in the denser target medium and may not expand properly.

 

[tim_w]

So you do then agree that as a bullet is in flight the stability increases as velocity decays/over time? I want to confirm this as in your post (#3 of the thread) you seem to be attempting to refute Mikecr's statement to that very fact. This is the major issue I believe we were all having issue with. (Ref quotes below)

There are a couple errors in this (perspective-wise).

1. A bullet that groups at all at 100yds will not hit a tumbling concern again until transonic. This, because gyroscopic stability increases as a bullet travels down range, all the way to transonic. The biggest free flight destabilizing moment is muzzle release. This is why bullets that will tumble generally do so immediately (within 10yds). They don't just decide to tumble on their own later.

To which you replied with your examples of shooting your bullet here and further comments.

Beg to differ. Early pn we made a 320 gr .338 that from a 1:9 twist at 100 yds at 60 degrees grouped one hole for 5 shots. Later in the winter at 5 degrees we shot the same bullet to 500 yds and every hit was sideways. Clearly the air was denser and there was a progressive tumbling that developed as the bullet traveled down range.It is the spin of the bullet that gives it its gyroscopic stability and long bullets have to be spun faster to maintain stability. Discussed the issue with some ballistisian from Hornady who said that was impossible, yet we obsrved it plain as day. If you take the JBM Stability Calculator and progressively increase the atmospheric pressure in the calculator you will see that the stability factor decreases. Do the opposite and it increases. Inadequately stabilized bullets will definitely tumble in gel if marginally stable in air. Why do you suppose subsonic bullets need tighter twists to stabilize? Gyroscopes become more stable the faster you spin them, and as they lose angular momentum they become more unstable. The basic gyroscopic principle is that a spining gyroscope resists torquing forces perpendicular to the spin axis. Bullets shot from rifled barrels have spin axes collinear with the direction of flight.

The part in bold is what we are in conflict with as was I am confident, the Hornady Ballictican you spoke to. No where in the rest of your post do you supply support for bullets loosing stability over TOF (time of flight).

You mention using JBM calculator and changing air density and seeing a corrlating drop in SG. I assume you are referring to the Modified Point Mass Trajectory calculator? First there are some accepted standards when it comes to gyroscopic stability factor or SG. Thru many real world controlled studies certain SG thresholds have been established. We only really need to reference two. If a properly cdesigned and constructed bullet has an accurately computed SG of 1.5 or higher for a traditional copper cup and lead core bullet it ensures full stability in all conditions. A mono copper or similar alloy bullet with a SG of 2.0 or higher will also be similarly stable in all conditions. I reference this as it can be used when interpreting the stability SG numbers in the JBM MPMT calculator's output..

Input whatever numbers you want for the bullet design or better yet just leave the defaults for this example. Include the point mass trajectory output and stability column by checking the last box on the left bottom just above the calculate button. Run the example. Look at the Trajectory column. Notice how with the increase in distance the SG number increases significant well above the 1.5 ideal threshold. Infact the default is ideal. The bullet has a SG 1.29 as it leaves the muzzle. By 100yd it's SG 1.42 (very close to tgat ideal 1.5) Jump out to 500yd and we have and SG 2.29. Way above the SG needed for not only full stability but maximum COF.

Now increase air density or decrease temp and allow the cal to adj to mimick the change in your live fire test from 60°F to 5°F.

Yes you will see a decrease in SG but look at the actual numbers as you increase distance specially 500yd as in your test. You will see SG at that distance/TOF the SG is way above the 1.5 threshold. Manipulate the numbers so at air density for 60°F has a SG of say 1.2-1.3 barely stabile. Look at the SG at 100 and 500 yds. You can see the bullet easily has a SG above 1.5 @ 500 yds. Stability always increases. A bullet can not be stabke enough to shoot bugholes at 100yds but hit sideways at 500yds Now adj temp to 5°F and see what the SG would be at 100 and 500 yds. You will see the bullet now clearly is below any SG that could afford stable flight. It may actually reach a SG @ 500 yd that could be stable if the bullet had not already reach a point of unrecoverable precession and yaw. No distance not 100 or 500 yds would ever produce a tight group with nice round holes. Basically an unrecoverable wobble.

As can be seen the JBM MPMT does not support but refutes your claim of stability decreasing with increased distance/TOF.

(Just using arbitrary numbers) Here is a hypothetical example of the ratio and relationship of twist rate velocity and bullet rpms looking at exiting the muzzle and at 1000yd:

A bullet from a 7.2 twist barrel with a MV of 3k fps and 300k rpm at a 1000 yd could have a hypothetical vel 1500 fps and 284k rpms. Vel decreasing 50% rotational rpm only 6.7% decrease. The V/RPM ratio went from 1:100 to 1:186. An 86% in ratio of vel to rpm. This would be the same stability at tge muzzle as if you you launched the same bullet at MV 1500fps from a 3.8 twist barrel. I think it's safe to say as long as a bullet is stable enough to print round holes at 100 yds it stablity will only increase from there and significant so the longer the TOF.

Addressing wound ballistics: This info was obtained from reference: Conventional Warfare: Ballistics, Blasts, and Burn Injuries. Chapter 4 The Physics and Biophysics of Wound Ballistics. pg 107-118

Borden Institute

U.S. Army Medical Center of Excellence, JBSA Ft. Sam Houston, Texas

medcoe.army.mil

In terms of rpms or more correctly the SG as it pertains to wound ballistics and flight path of bullets thru different media what we are really speaking about is coefficient of drag or CD. CD is based upon the ratio of the velocity of the given projectile (Vp) to the velocity of the speed of sound (Vs) thru a given medium. (VP/Vs). That medium can be anything but usually (air, water, muscle tissue, various organ tissue etc). This is how you arrive at the "Mach" number . Below M1 is subsonic above it is supersonic for travel thru/in a given medium. There is the transition phase "transsonic". Transsonic is between M0.8-M1.20. Starting high and working down CD is stable just below and thru M2. When it reaches transsonic CD increases dramatically 3-4x!!! (M0.8-M1.2). Hence my earlier statement about subsonic load mv vel and the reason for increased twist rate for increased rotational vel unless mv velocity is lowered below that threshold. M0.6-M0.7 and lower CD is again very stable until, you get way down, around 100-115fps thru air.

As far as I know lung tissue has the lower density of major mass in the body. It's the tissue with the lowest retardation force and thus a bullet can achieve actual supersonic vel in it. The retarding force of other tissue had retarding forces that are tens of thousands of times greater than air.

The last part to effect CD and least critical is the stretchiness or more correctly the viscoelastic properties of the medium a bullet travels in.. As this is all about terminal wound ballistics we are referencing flesh.

As most offical live testing data was done with swine as its very similar to human muscle tissue we have these numbers. Muscle tissue CD 0.45.

This then brings us back to bullet stability. In this case stability in muscle tissue. Bullets of course have horrible stability in tissue. To put it into perspective for a bullet to have equal stability in tissue as it does in air even if you coukd make that tissue perfectly consistent it would require you to increase rpms at impact vel by roughly 32 fold. Going back to my previous hypothetical example 284k rpm would need to be increased to a tad over 9 Million RPM. Never going to happen thus bullet SG as long as its stable has the least effect. Bullet design is far more critical. Look at military bullets used and how they tend to yaw within a few inches of penetration. Increased total wound channels volume from fragmentation from the forced imparted from yaw vs traditional expansion.